在现代区域防空体系中，地面防空装备的合理与有效部署尤为关键^[1]。部署方案的设计与执行效率，不仅直接影响着防空装备能否发挥出最大的实战能力，而且对于整个防空作战的空间战略布局、战术层面的实施，乃至最终的作战成效，均起着决定性作用^[2]。制定一套能够充分发挥防空装备战斗力的部署方案，已成为确保现代防空行动成功的关键要素之一^[3]。然而，面对广阔区域的防空需求，传统的部署方法，如枚举法^[4]、分支定界法^[5]等，在应对多样化、大规模的防空系统部署时，常常遭遇计算复杂度高、耗时长等问题^[6]。鉴于现代战场环境的快速演变与对部署策略实时响应能力的迫切需求，研究高效部署优化算法及策略，一直是学术界和军事研究领域关注的热点^[7]。

为提高传统防空装备部署策略的实时性，群智能优化算法在防空装备部署优化问题中得到了广泛研究^[8-10]：文献[8]利用简化粒子群算法在兵力部署解空间中进行快速寻优；文献[9]提出改进量子遗传算法以解决岛礁防空中防空武器部署的突出问题；文献[10]提出了基于烟花算法的要地防空多传感器部署优化方法以解决传统的多传感器部署规划不适用于要地防空任务场景的问题。

在这些群智能优化算法中，人工蜂群（artificial bee colony, ABC）算法不易陷入局部最优、算法结构简单易于实现，还具备较为强大的搜索能力^[11−12]。在军事研究领域，ABC算法体现了显著的优化能力^[11−14]：文献[11]提出一种改进的自适应离散多目标ABC算法，将锦标赛选择取代轮盘赌，并且设计一种自适应改进机制以针对大规模武器目标分配问题；文献[13]提出一种改进ABC算法，其利用先验知识来引导种群初始化，并在ABC算法的基础上融合了向量编码方式、引导策略等改进措施；文献[14]提出一种按基因组搜索的改进ABC算法。由此可见，ABC算法因其显著的优势已被广泛应用。在地面防空装备部署中，ABC算法也备受青睐，文献[15]将ABC算法分为初始化阶段和优化阶段，提出了一种简化ABC算法的地面防空装备部署方法。在兵力部署问题中：文献[16]在ABC算法基础上建立两种新策略，通过针对性地设计和改进，提高ABC算法的迭代速度；文献[17]针对ABC算法在开发能力和收敛速度上的局限性，将ABC算法与遗传算法相结合，提出了一种改进遗传蜂群算法的部署方法。针对坦克阵地部署，文献[18]提出坦克阵地部署模型的ABC算法，对ABC算法进行有针对性的设计。

尽管文献[15−18]在一定程度上提高了部署策略的实时性，但实际地形对防空效能的影响并未得到充分考虑^[19]。实际上，数字高程模型（digital elevation model, DEM）作为一种区域地形起伏的数字化表达^[20]，蕴含了丰富的地形地貌信息。DEM提供的这些信息对防空装备部署大有裨益^[19]，且在一些研究中进行了应用^[21−24]：文献[21]根据DEM数据选择待部署位置，并用遗传算法进行部署；文献[22]对DEM进行处理分析，为气象站部署提供了地理信息支持；文献[23]使用DEM获取经纬度和数字高程信息，为天气雷达选址部署提供了技术支撑；文献[24]基于数字地形，分析部署区域地形条件，为兵力部署提供了理论支撑。可见，DEM在一定程度上提升部署策略的合理性^[25−27]。受DEM丰富的数字地形信息启发，将DEM融入到ABC算法中，有望在增强地面防空装备部署实时性的同时改善其合理性。

为此，本文提出一种基于数字高程模型和人工蜂群算法的地面防空部署策略，将DEM作为先验信息，引导ABC算法的迭代寻优过程，旨在快速寻找地面防空装备部署方案的同时，改善部署方案的合理性。本文的主要贡献如下。

1）利用DEM数据作为先验信息对部署区域进行预处理。在算法初始化阶段开始前，根据部署区域的DEM数据分析处理，得到优化因子，并且初步筛选部署位置，以充分考虑地形对部署的影响从而提高部署方案的合理性。

2）自适应邻域优化策略。利用优化因子对邻域优化过程进行引导，根据优化因子的大小，对部署方案进行集中性邻域优化和多样性邻域优化。较大的优化因子会引导更集中性的搜索，以寻找更优部署方案，从而提高部署方案的质量；较小的优化因子会引导更多样性的搜索，以寻找更多部署方案，从而提高全局搜索的效率。

3）给定防空效能指标的提前停止策略。研究方法还根据预设的防空效能指标对产生的部署方案进行评判，若产生符合防空效能指标的部署方案则直接停止算法迭代。提前停止策略的引入，不仅可以减少算法运行时间，提高算法实时性，而且能确保生成的部署方案满足防空需求。

经过改进后的邻域优化机制，能依据优化因子的具体数值动态调整对不同地面子区域的优化权重。优化因子的融入，有效增强了算法的自适应能力，既保证了部署方案的高质量，又提高了部署方案的多样性。仿真结果表明，相比于经典群智能优化算法，本文方法在加速了寻优过程的同时，使产生的部署方案符合实际部署条件。

1.   地面防空装备部署场景与问题形成

1.1   部署场景

1）地面区域划分。

防空装备的种类为$T$类，第$t$（$t = 1,2, \cdots ,T$）类防空装备有${D_t}$个防空装备，于是，防空装备的总数量为

需要将$ {N_{\text{D}}} $个防空装备在地面区域内进行部署。将地面区域划分为${N_{\text{A}}}$个子区域，子区域集合$ \mathcal{A} $可表示为

式中${{{A}}_j}$表示第$j$个地面子区域。不失一般性，假设每个子区域只能部署一个防空装备^[28]。

2）部署场景描述。

由于我国地域辽阔，要地众多，对于防空装备部署而言，地面子区域个数通常远远超过防空装备的总数量，即${N_{\text{A}}} \gg {N_{\text{D}}}$。因此，为抵抗来袭飞机，需要在划定的$ {N_{\text{A}}} $个地面子区域上选择${N_{\text{D}}}$个子区域部署${N_{\text{D}}}$个防空装备^[2]。

为方便起见，将${N_{\text{D}}}$个设备组成设备集合$ {\mathbf{\gamma }} $表示为

假设所有可能的部署方案的总数为$ {N_{\text{S}}} $，用$ {{S}} $表示$ {N_{\text{S}}} $个防空装备部署方案全集，有

在第$i$个部署方案${{{S}}_i}$（$ i = 1,2, \cdots ,{N_{\text{S}}} $）中，将第$i$个部署方案的第$j$个地面子区域表示为${{{A}}_{i,j}}$。于是，选出的${N_{\text{D}}}$个地面子区域集合$ {\widetilde {\mathcal{A}}_i} $，可表示为

于是，第$i$个部署方案${{{S}}_i}$可用${{{A}}_{i,j}}$和$ {\gamma _j} $表示为

本文部署策略的目标是：针对特定的地面子区域与给定数量的防空装备，生成能够兼顾高实时性和合理性的部署方案。

3）部署方案评价指标。

在现代防空作战中，部署方案通常倾向于追求火力纵深、杀伤区重叠次数以及火力密度最大化，以达到最大程度消灭空中威胁的效果^[7]。然而，根据文献[29]，防空效能评估现况还存在评估方法不够客观、评估指标不能直接反应作战效能等问题。为此，本文以有效性分析、合理性分析和优化因子影响分析为示例，阐述防空效能评价指标。

①防空效能。

根据文献[30−32]，防空效能定义为毁伤概率和命中概率的乘积。第$i$个设备部署方案$ {{\mathbf{S}}_i} $的防空效能可表示为

式中：$ {P_{\text{E}}}\left( {{{{A}}_{i,j}},{\gamma _j}} \right) $表示第$i$个部署方案在地面子区域${{{A}}_{i,j}}$部署防空装备$ {\gamma _j} $的防空效能，可表示为

其中，$ {P_{\text{E}}}\left( {{{{A}}_{i,j}},{\gamma _j}} \right) $和$ {P_{\text{D}}}\left( {{{{A}}_{i,j}},{\gamma _j}} \right) $分别表示地面子区域${{{A}}_{i,j}}$部署防空装备${\gamma _j}$时的命中概率和毁伤概率^[32−33]，${\omega _{i,j}}$表示第$i$个部署方案中地面子区域${{{A}}_{i,j}}$的威胁系数。

②命中概率。

根据文献[32]，式(8)中的命中概率$ {P_{\text{H}}}\left( {{{{A}}_{i,j}},{\gamma _j}} \right) $定义为

式中$s$表示来袭飞机暴露面积。这里，用半径为${r_{\text{p}}}$的圆表示该暴露面积，即$s = \text{π} r_{\text{p}}^2$。在式(9)中，$ \sigma _j^2\left( {{{{A}}_{i,j}},{\gamma _j}} \right) $可以表示为

其中，${\sigma _j}$表示第${\gamma _j}$个防空装备脱靶量的圆标准差，$R\left( {{{{A}}_{i,j}}} \right)$为地面子区域${{{A}}_{i,j}}$的位置参数，${c_1}$、${c_2}\left( {{\gamma _j}} \right)$为拟合常数。

③毁伤概率。

根据文献[33]，以导弹为例，式(8)中的毁伤概率$ {P_{\text{D}}}\left( {{{{A}}_{i,j}},{\gamma _j}} \right) $定义为

式中：$\sigma $表示导弹制导误差；${r_0}$表示制导误差的系统误差分量；$r$表示脱靶量；$R$为受地面子区域影响的杀伤规律参数；$ {{{I}}_0}\left( \cdot \right) $为零阶贝塞尔函数。毁伤概率作为地面防空装备部署中的重要指标之一，关系到诸如生存能力、部署方案的成败等^[34]。式(11)中，杀伤规律参数$R$可用方案$ {{{S}}_i} $中参数${{{A}}_{i,j}}$和$ {\gamma _j} $进行表征。假设表征函数为${f_{{\text{Break}}}}\left( { \cdot , \cdot } \right)$，则第$i$个部署方案中，在地面子区域${{{A}}_{i,j}}$部署防空装备$ {\gamma _j} $的杀伤规律为

④位置威胁系数。

在相对平坦的平原地区执行防空部署任务时，地形因素对防空装备的影响体现得并不显著。然而，在进行野战防空部署，特别是在崎岖多山的地貌环境中，地形条件则会对防空装备的运作造成实质性的影响^[35]。例如，复杂的地形可能会导致炮弹发射时受到自然障碍物的遮蔽，这直接影响到防空装备的有效覆盖范围及拦截效率，从而对其防空效能产生重大影响。本文在利用DEM辅助ABC算法优化的同时，引入位置威胁系数${w_{m,n}}$，将DEM提供的海拔信息深入应用于考量防空装备在实际作战时可能出现的射界遮挡问题，从而提升优化结果的精确性和实用性。

在讨论防空装备的有效防御范围时，将其火力覆盖区域抽象建模为一个理论上的扇形几何域。实际的火力覆盖区域是连续分布的，然而，在对其进行定量优化分析时，就必须要进行量化处理。根据文献[36]，对防空装备的火力覆盖进行网格离散化处理，如图1所示。其中：上图表示对防空装备火力覆盖进行网格化处理，并且网格应划分的足够小，旨在确保每个网格交叉点能够精确代表实际地理空间中被火力覆盖的点；下图以矩阵抽象模型的方式对防空装备的火力覆盖范围进行了概要表示。矩阵元素值${w_{m,n}}$被赋予了特定含义：若${w_{m,n}} = 1$，则表示相应地面子区域处于火力覆盖范围内；若${w_{m,n}} = 0$，则代表该地面子区域未被火力所覆盖；若${w_{m,n}} = - 1$，则表示该地面子区域由于存在障碍物而无法实现火力覆盖。

图  1  火力覆盖示意图

Figure  1.  Schematic diagram of fire coverage

下载: 全尺寸图片 幻灯片

根据${w_{m,n}}$求出未存在遮挡的火力覆盖值${w_{{\text{normal}}}}$和存在遮挡的火力覆盖值${w_{{\text{abnormal}}}}$，分别表示为

式中，$M$、$N$分别表示部署区域的横向、纵向的子区域个数。根据${w_{{\text{normal}}}}$和${w_{{\text{abnormal}}}}$，得到火力覆盖因子$\varpi $，表示为

根据火力覆盖因子$\varpi $的大小，式(8)中的位置威胁系数${\omega _{i,j}}$定义^[28] 为

1.2   问题形成

部署方案的设计与执行是一个涉及诸多变量动态平衡的过程，尤其是在资源有限与威胁持续变化的现实条件下，如何权衡各项指标以实现防空效能的最大化，就成为了一个亟待解决的优化问题^[37]。

1）优化问题形成。

为保证部署方案的有效性，产生的部署方案应保证防空效能最大。即，从$ {N_{\text{S}}} $个部署方案中选出最大防空效能的部署方案，表示为：

式中：$\left( {{\text{C1}}} \right)$表示产生部署方案的防空效能应不小于防空效能门限；$ \left( {{\text{C2}}} \right) $表示产生的部署方案$ {{{S}}_i} $应是所有部署方案集合$ {{S}} $中的子集，部署方案的地面子区域$ {{{A}}_{i,j}} $应在给定地面子区域集合$ \mathcal{A} $中选取，并且部署的防空装备$ {\gamma _j} $是在给定的防空装备集合$ {\mathbf{\gamma }} $中选取。

2）ABC算法求解可行性。

尽管相同类型的设备具有相似的性能特征，然而，当这些设备部署在不同的地面子区域时，可能因为多种因素而呈现出差异化的性能表现。因此，从$ {N_{\text{A}}} $个地面子区域选出${N_{\text{D}}}$个子区域部署${N_{\text{D}}}$个不同防空效能的防空装备的部署方案总数$ {N_{{\text{Sch,Total}}}} $可表示为

广袤的部署区域会造成地面子区域数${N_{\text{A}}}$非常大，在${N_{\text{A}}}$个地面子区域中部署${N_{\text{D}}}$个不同防空效能的防空装备的部署方案总数$ {N_{{\text{Sch,Total}}}} $也会非常大。例如，当${N_{\text{A}}} = {10^3}$，${N_{\text{D}}} = {10^2}$时，则共有部署方案总数为

根据上述示例，若采用枚举法全局搜索最优部署方案需要对比不少于10²⁹⁷种部署方案。这种数量级的方案寻优，计算资源消耗巨大、处理延迟高，严重违背复杂多变战场环境对实时性的需求，难以实用。在实际的防空部署中，地面子区域数${N_{\text{A}}}$和防空装备数${N_{\text{D}}}$可能会比上述示例更大，寻求全局最优解在计算资源和时间成本上几乎不可能，无法满足实时性要求。更重要的是，耗费大量计算资源和时间成本得到的全局最优解，有时因过于理论化还难以匹配战场环境的具体特征，缺乏实战应用的合理性。

鉴于ABC算法具有不易陷入局部最优、算法结构简单易于实现，以及具备较为强大的搜索能力等优点^[11-18]。本文采用ABC算法对地面防空装备部署方案进行迭代寻优。为更有效地应用ABC算法解决地面防空装备部署问题，进一步改善其收敛速度与部署方案的合理性，考虑将DEM融入ABC算法，利用DEM对ABC算法进行引导，进一步减少算法的迭代过程，加快其收敛速度，并增强部署方案的合理性。因此，本文立足于防空效能最优的目标，利用DEM数据以强化算法求解的实用性和适应性，并在此基础上对ABC算法进行改进，旨在求解出防空效能最大化的部署方案。

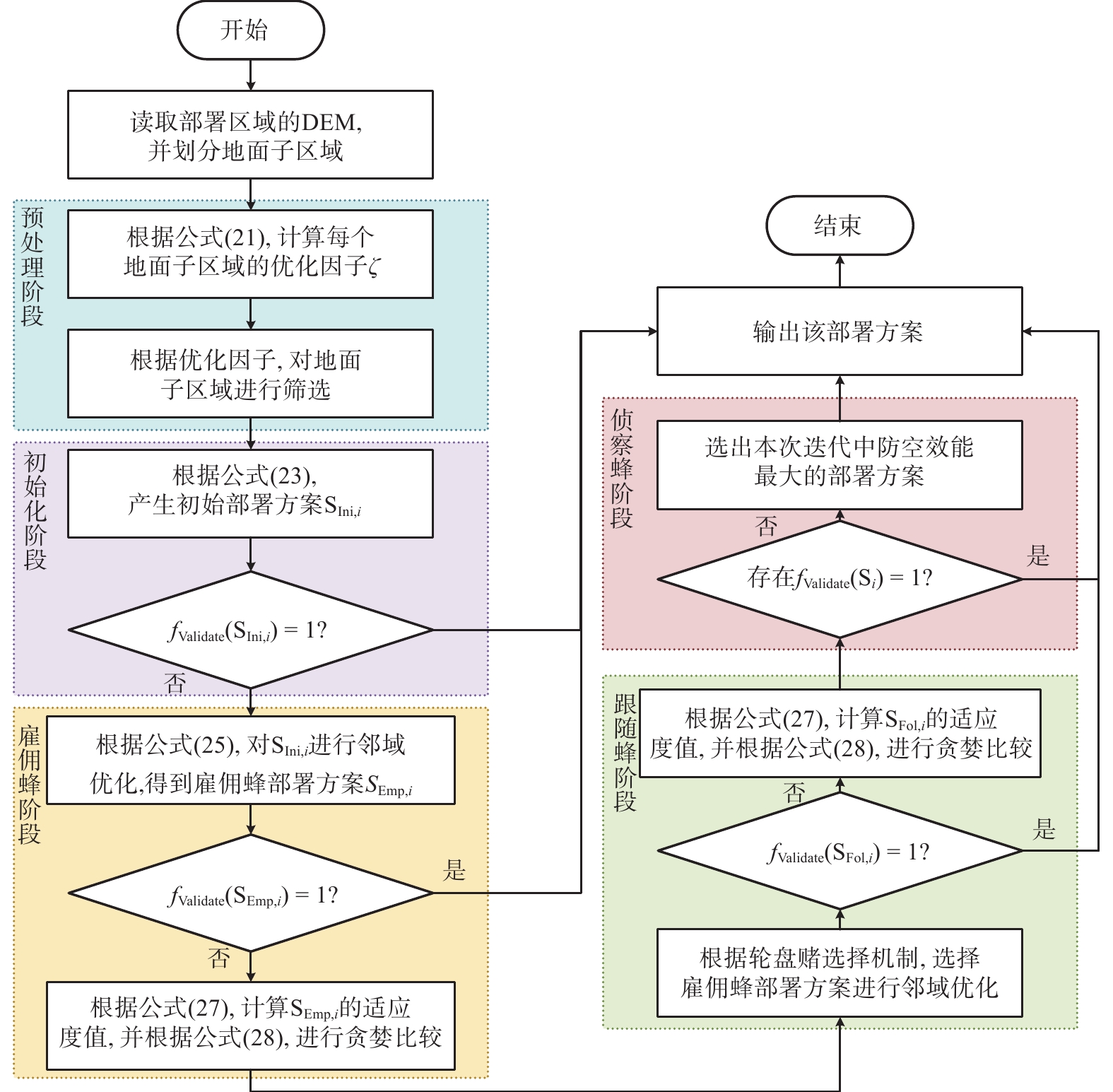
2.   基于DEM和ABC算法的地面防空装备部署方法

以防空效能为示例，本文提出的求解算法充分考虑了实际地形地貌、海拔差异等因素，利用DEM建立了一个更具有实际物理意义、更高效能的部署优化模型。DEM的引入使得算法能够更全面地评估不同地面子区域的部署适宜性，并在实际应用中更灵活地应对战场环境的复杂性，从而更有效地提高地面防空装备部署方案的防空效能。

2.1   预处理阶段

目前，现有的ABC算法在进行优化问题求解时，并未对已有的数据进行加工处理，而是直接进行随机种群（解集）初始化。这种随机初始化处理虽然在一定程度上增加了解集多样性，避免全局最优解，但是，对于解空间十分庞大的问题，随机初始化处理的效果就不尽如人意^[38-39]。

因此，本文在进行初始化前，利用DEM数据对需要进行部署任务的地面区域进行分析，根据地理位置的海拔高度得到优化因子，得到所有子区域的位置优化因子后，再进行种群初始化。这样在提高算法求解效率、减少计算复杂度的同时也提高了部署方案的适用性。

对所有地面子区域获取海拔数据，计算平均海拔高度$\bar h$，表示为

其中，第$i$个地面子区域的优化因子${\zeta _i}$表示为

图  2  地形DEM数据三维图

Figure  2.  Terrain DEM data three-dimensional map

下载: 全尺寸图片 幻灯片

由于地形复杂性、海拔高度以及其他环境限制等因素，地面防空装备在执行部署任务时十分困难。特别是在山地地形下，自然地貌对部署任务的挑战显著增加。例如，在低洼地带易遭水患、高海拔处难于运输且易暴露。

因此，本文在根据海拔信息得到${N_{\text{A}}}$个优化因子后，对${N_{\text{A}}}$个优化因子进行筛选，直接删除较小的优化因子和相邻差距较大的优化因子对应的地面子区域，从而避免了海拔太高或太低的地面子区域难以运输防空装备、部署子区域有障碍物遮挡的问题，增强了部署的合理性。

2.2   初始化阶段

采用与经典ABC算法相同的初始化策略^[15]，随机产生部署候选解，得到初始部署方案，第$i$个部署方案中第$j$个地面子区域${{{A}}_{i,j}}$的随机初始化过程表示为

式中：${j_i}$表示第$i$个部署方案的第$j$个地面子区域编号；${\text{round}}\left( x \right)$表示对$x$的值四舍五入；$\varphi $是$\left[ {0,1} \right]$范围内均匀分布的随机数。

根据式(22)，得到由${N_{\text{D}}}$个地面子区域和防空装备组成的防空部署方案，其中，第$i$个初始部署方案$ {{{S}}_{{\text{Ini,}}i}} $表示为

得到初始部署方案后，根据部署方案的防空效能、地面子区域的地形地貌、路网信息等条件作为部署指标，对部署方案进行校验，表示为

若产生的部署方案校验合格，即$ {f_{{\text{Validate}}}}\left( {{{{S}}_i}} \right) = 1 $，则停止算法迭代，将当前的部署方案直接输出，从而改善实时性；否则，进行算法后续处理。

2.3   雇佣蜂阶段

在解决部署方案求解问题时，经典ABC算法中雇佣蜂与跟随蜂阶段的邻域搜索机制存在固有的随机性质，其适用性并不理想。为此，本文巧妙地引入了在预处理阶段获得的优化因子，用以引导并改进邻域优化步骤。此外，经过邻域优化阶段形成的新部署方案会进一步接受部署指标的校验判断：若新方案成功满足预设的部署指标，则算法即时终止当前迭代过程，以改善实时性不高的问题。

经典ABC算法在雇佣蜂阶段对初始化产生的每个食物源进行探索开发^{[40 − 41]}，在此基础上，本文方法利用预处理阶段的优化因子$\zeta $，对第$i$个部署方案中第$j$个地面子区域${{{A}}_{i,j}}$的邻域优化过程表示为

得到的第$i$个雇佣蜂部署方案$ {{{S}}_{{\text{Emp,}}i}} $表示为

得到$ {{\mathbf{S}}_{{\text{Emp,}}i}} $后，根据公式(24)对部署方案进行校验。若产生的部署方案校验合格，即$ {f_{{\text{Validate}}}}\left( {{{{S}}_i}} \right) = 1 $，那么停止算法迭代，将当前的部署方案直接输出；否则，进行算法后续处理。

在邻域优化完成后，计算部署方案的适应度值，供跟随蜂阶段轮盘赌选择。部署方案的适应度值计算表达式为

其中，${\mathrm{fit}}\left( {{{{S}}_i}} \right)$表示第$i$个部署方案的适应度值。

完成适应度计算后，雇佣蜂会通过贪婪选择^[42]的方式进行食物源的筛选，即选择适应度高的部署方案，为

2.4   跟随蜂阶段

在跟随蜂阶段，与经典ABC算法相同，本文方法采用轮盘赌选择机制^[42]来选择不同部署方案进行此阶段的邻域优化，对$ {{{S}}_{{\text{Emp,}}i}} $根据公式(25)进行邻域优化处理。随后，对于经过雇佣蜂阶段邻域优化后所产生的新的跟随蜂部署方案$ {{{S}}_{{\text{Fol}}}} $，会进一步依据公式(24)对其进行部署指标评判，并按公式(28)进行贪婪比较，确保方案的有效性和适用性。

2.5   侦察蜂阶段

在侦察蜂阶段中，本文方法通过引入优化因子对部署方案求解，增强了部署策略的针对性与多样性。此外，每个阶段都根据公式(24)对产生的部署方案进行部署指标判决，无需额外考虑邻域优化限制次数的约束^[40]。此阶段分2种情况对迭代产生的部署方案进行讨论。

情况1：如果此次迭代过程中没有产生满足部署指标即公式(24)的部署方案，那么侦察蜂阶段会选择本次迭代过程中产生的防空效能最大的部署方案作为输出。

情况2：如果此次迭代过程中产生了满足部署指标的部署方案，那么侦察蜂阶段会把满足部署指标的部署方案作为输出。

本文方法的流程图如图3所示，对应的算法流程如图4所示。

图  3  算法流程图

Figure  3.  Algorithm flow chart

下载: 全尺寸图片 幻灯片

图  4  本文算法

Figure  4.  The algorithm

下载: 全尺寸图片 幻灯片

3.   实验仿真

假设某防空小队需要在某区域需要进行部署任务，给定仿真条件^[41]如表1和表2所示。

表  1  防空装备参数

Table  1.  Air defense equipment parameters

防空装备类型	个数	制导误差/m	系统误差分量/m	脱靶量/m
${D_1}$	30	$ \left[ {0,50} \right] $	$ \left[ {0,30} \right] $	$ \left[ {0,30} \right] $
${D_2}$	50	$ \left[ {0,100} \right] $	$ \left[ {0,50} \right] $	$ \left[ {0,50} \right] $
${D_3}$	20	$ \left[ {0,150} \right] $	$ \left[ {0,80} \right] $	$ \left[ {0,70} \right] $
${D_4}$	50	$ \left[ {0,200} \right] $	$ \left[ {0,100} \right] $	$ \left[ {0,90} \right] $

下载: 导出CSV 

| 显示表格

表  2  仿真参数

Table  2.  Simulation parameters

参数	取值
防空装备种类	$T = 4$
防空装备总数	${N_{\text{D}}} = 150$
部署区域范围	$X = 3061,Y = 3061$
地面子区域数	${N_{\text{A}}} = 12967201$
防空效能指标	${P_{{\text{Th}}}} = 0.97$
杀伤规律参数	$R \in \left[ {0,1} \right]$

下载: 导出CSV 

| 显示表格

3.1   有效性分析

本文方法进行1000次迭代后得到的结果与经典群智能优化算法^[42-46]进行1000次迭代后得到的结果进行比较，得到的防空效能与迭代次数仿真结果如图5所示。

图  5  有效性分析

Figure  5.  Effectiveness analysis

下载: 全尺寸图片 幻灯片

1）相较于经典群智能优化算法，本文方法在寻求部署方案的过程中，能更快地产生满足${P_{{\text{Th}}}}$的部署方案。具体来说，在给定部署区域以及表1和表2条件的情况下，本文方法在经历197次迭代即能得到满足防空效能指标的部署方案，经典ABC算法、遗传算法和蚁群算法分别经历421、500、467次迭代才能得到满足防空效能指标的部署方案，粒子群优化算法甚至在1000次迭代中没有产生满足防空效能指标的部署方案。

2）相较于经典群智能优化算法，本文方法在寻求部署方案的过程中，能产生更高防空效能的部署方案。具体地，本文方法在经历319次迭代时得到0.9728防空效能的部署方案，而经典群智能优化算法在1000次迭代内产生部署方案的防空效能都在0.9700左右。

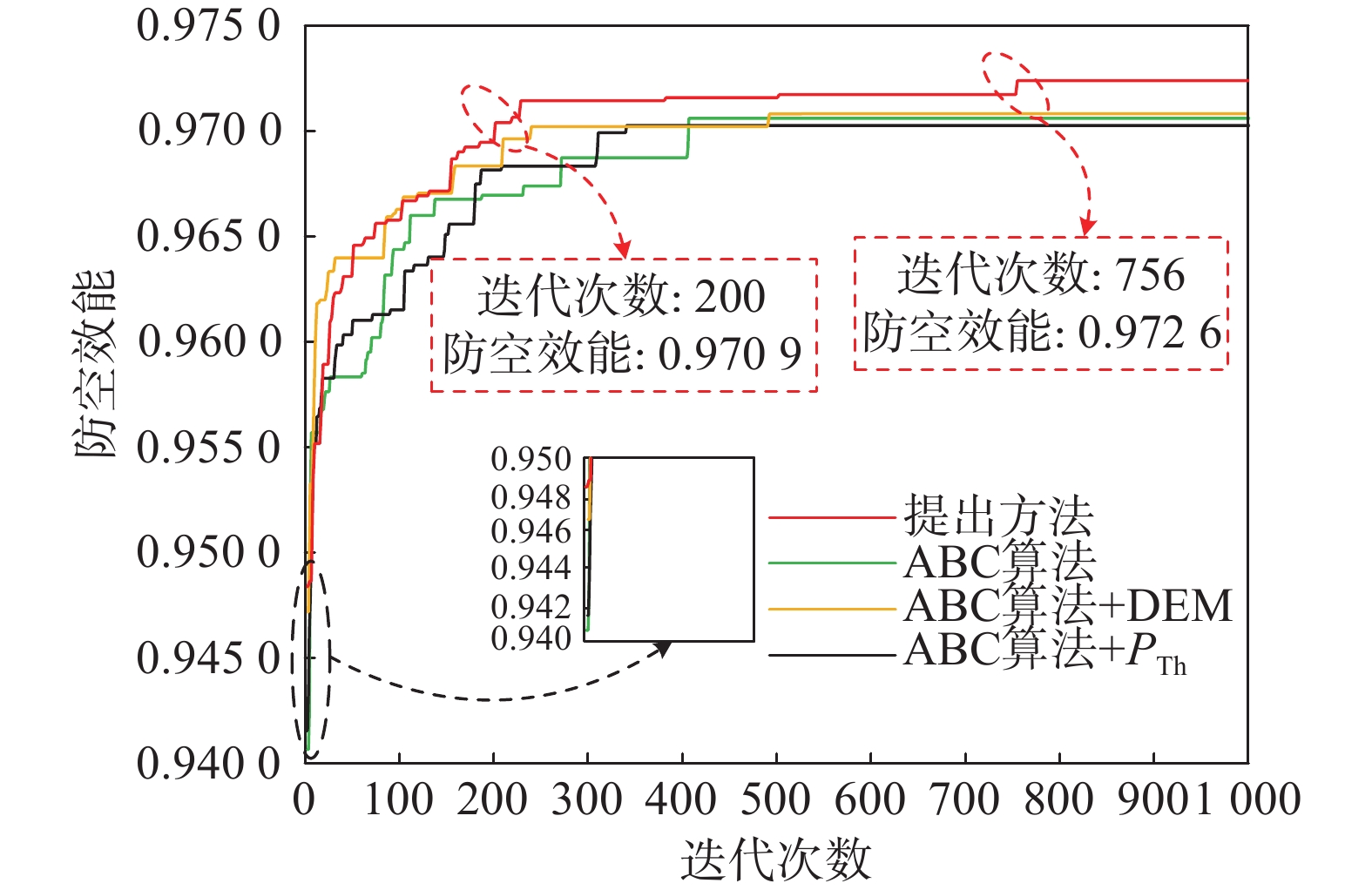
3）相较于经典群智能优化算法，本文方法产生的初代部署方案具有更高的防空效能。具体而言，在迭代初期，本文方法产生的部署方案具有更高的防空效能，其数值达到0.9483，相比之下，经典群智能优化算法产生的防空效能均未能超过0.9450。

此外，将本文方法与经典ABC算法、经典ABC算法+DEM、经典ABC算法+${P_{{\text{Th}}}}$进行比较，其结果如图6所示。

图  6  有效性分析

Figure  6.  Effectiveness analysis

下载: 全尺寸图片 幻灯片

1）本文方法在初代产生的部署方案具有更高的防空效能。此外，经典ABC算法与DEM结合的方法在初代产生的部署方案的防空效能高于经典ABC算法和经典ABC算法+${P_{{\text{Th}}}}$。具体地，本文方法的初代部署方案的防空效能为0.9489，经典ABC算法与DEM结合方法的初代部署方案的防空效能为0.9468，经典ABC算法和经典ABC算法+${P_{{\text{Th}}}}$产生的初代部署方案防空效能都在0.9450以下。其原因在于，DEM数据作为先验信息，引导部署方案的迭代寻优过程，使得初代部署方案的防空效能更高。

2）本文方法在迭代寻优过程中，能更快产生满足防空效能指标的部署方案。具体来说，本文方法在200次迭代就产生了满足防空效能指标的部署方案，经典ABC算法、经典ABC算法+DEM、经典ABC算法+${P_{{\text{Th}}}}$分别在407、237、311次迭代才产生满足防空效能指标的部署方案。具体来说，迭代次数减少意味着算法能以更快的速度收敛至有效解，从而大幅缩短部署方案生成时间。其原因在于，本文方法将DEM数据融入ABC算法中，将其作为先验信息，引导部署方案的迭代寻优过程，进而显著提升了寻优效率与部署方案的产生速度。

3）本文方法能产生更高防空效能的部署方案。在1000次迭代仿真中，本文方法经过756次迭代产生的部署方案防空效能为0.9726，其他3种方法在1000次迭代中产生的部署方案其防空效能均在0.9700附近。

由图5和图6的有效性分析图可以看出，本文方法能显著减少算法迭代次数，迭代次数的减少直接降低了计算成本，从而提高了实时性。

3.2   合理性分析

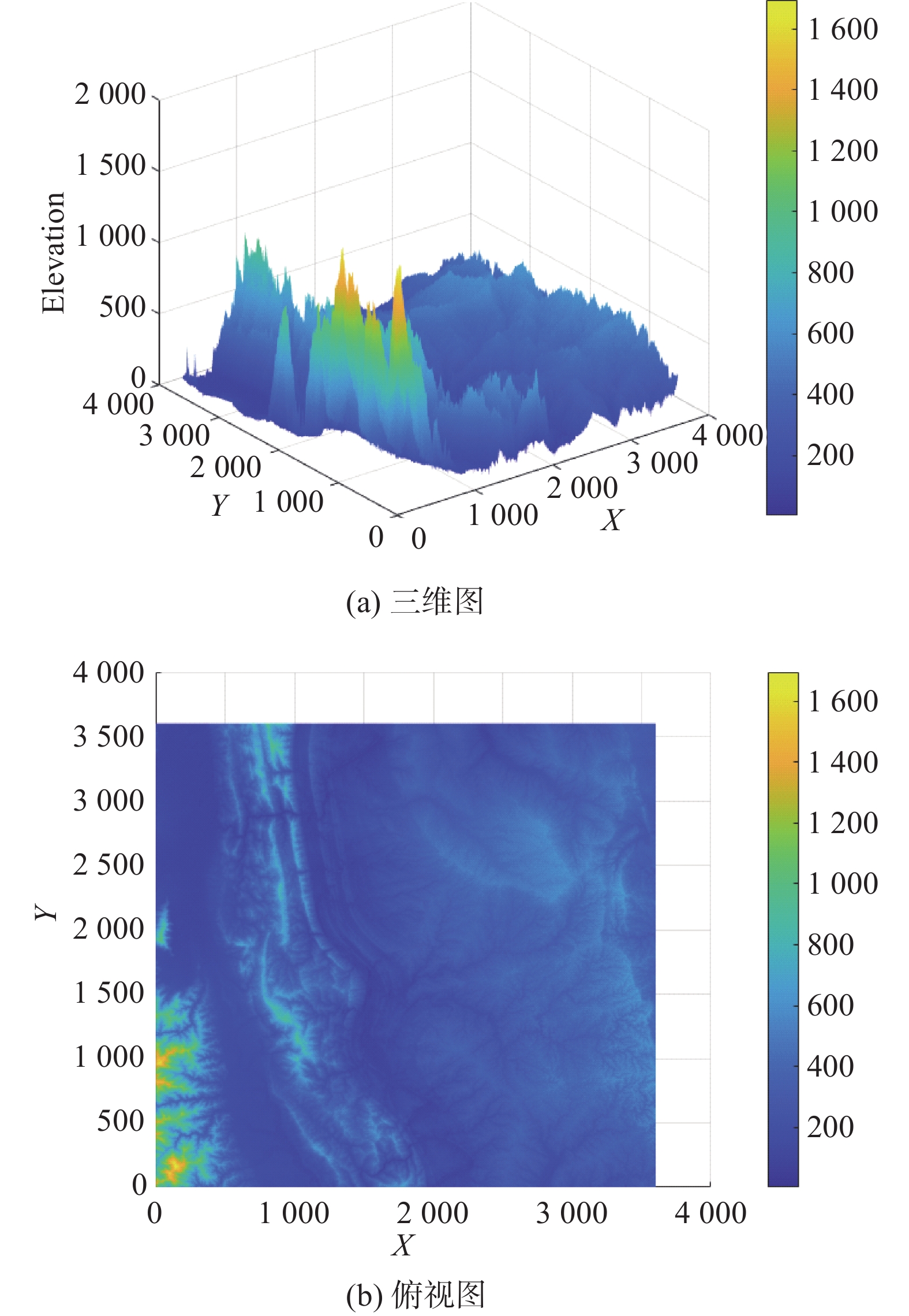
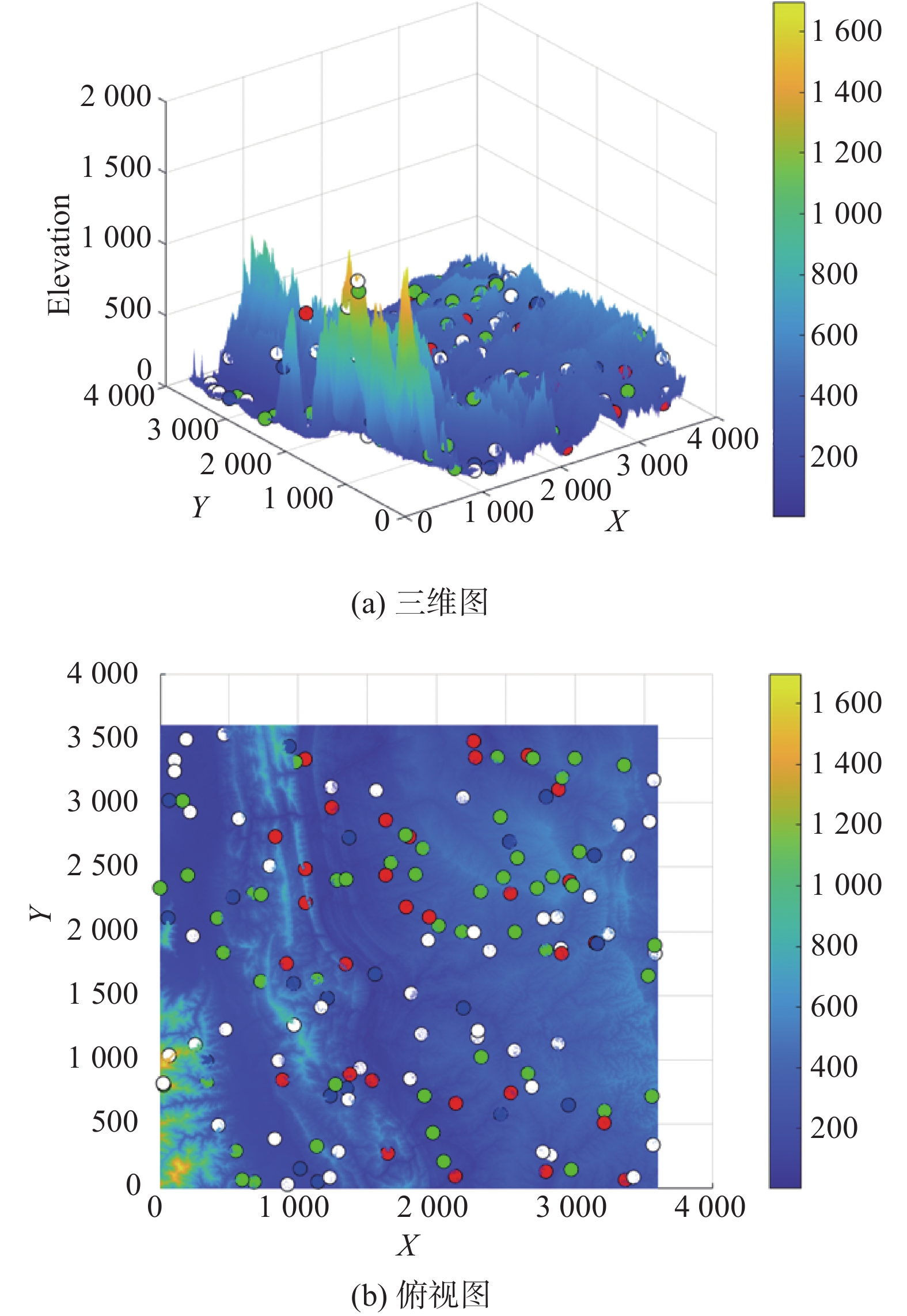
DEM对部署方案的合理性有一定的影响。图7和图8给出了相应的仿真结果，其中4类设备分别用红、绿、蓝、白四种颜色的点表示。

图  7  本文方法部署方案DEM数据图

Figure  7.  Deployment scheme diagram of the proposed method with DEM data

下载: 全尺寸图片 幻灯片

图  8  经典ABC算法部署方案DEM数据图

Figure  8.  Deployment scheme diagram of the classic ABC algorithm with DEM data

下载: 全尺寸图片 幻灯片

图7和图8分别为运用本研究方法所获得的部署方案在DEM数据下的可视化表现和运用经典ABC算法所获得的部署方案在DEM数据下的可视化表现。

可以看出，在应用经典ABC算法时，部署方案中一些部署点在海拔约为1600 m和200 m的高度区域。然而，本文方法采用DEM作为先验指导信息后，生成的部署方案不再包含位于1600 m和200 m高度位置的部署点，而是遵循地形信息实现了更为合理的部署。具体地，本文方法通过分析部署区域的平均海拔，对部署位置进行筛选，避开易受雨季影响的低洼地带以及运输困难容易暴露的高海拔地区。这不仅显著提升了部署方案的地理适宜性，更提高了实战合理性。合理性的提升不仅体现在对潜在风险的规避上，更在于确保了防空设备的高效性与安全性，从而为实现整体战略目标奠定了坚实的基础。

3.3   优化因子影响分析

预处理阶段得到的优化因子对部署方案的求解寻优过程也存在影响。在上述条件的基础上，通过对预处理阶段的优化因子大小进行筛选，将优化因子从大到小排序，进行了5组实验，即分别考虑了前$10\% $、前$20\% $、前$50\% $、前$90\% $的${\zeta _i}$以及不对${\zeta _i}$进行筛选。图9给出了相应的仿真结果。

图  9  不同${\zeta _i}$占比影响分析

Figure  9.  Analysis of thedifferent proportions of ${\zeta _i}$

下载: 全尺寸图片 幻灯片

1）优化因子对初代产生部署方案的防空效能有明显影响。具体地，前$10\% $的${\zeta _i}$产生的部署方案在第一次迭代产生部署方案的防空效能就达到了0.9588，而不对${\zeta _i}$进行筛选产生的部署方案防空效能为0.9489。

2）优化因子对算法迭代产生部署方案的防空效能有提升效果。例如，前$10\% $的${\zeta _i}$经243次迭代后产生了防空效能为0.9783的部署方案，而不对${\zeta _i}$进行筛选经341次迭代产生了防空效能为0.9730的部署方案。

4.   结论

本文利用DEM，并根据给定防空效能门限对部署方案进行校验，研究预先进行阵地筛选的地面防空装备部署优化ABC算法，根据需要进行部署任务区域的DEM得到优化因子，利用优化因子引导邻域优化过程，并且对产生的部署方案进行防空效能指标评判，通过利用DEM对部署区域筛选，提前排除不适合部署的区域，减少算法解集空间，提高算法实时性的同时，增强部署方案的合理性。本文研究为地面防空装备的部署问题提供了一种新方法，可以改善收敛速度并提高防空效能。