双频驱动双转子振动系统控制同步特性研究
Investigation on Controlled Synchronous Characteristics of Dual-Rotor Vibration System Excited with Double-Frequency
-
摘要:
针对石油工程中同频钻井振动筛时常出现筛网堵塞,导致钻井液遗失并增加钻井成本的问题,提出一种双频驱动双转子控制同步振动系统,使筛网表面的物料在单周期内受到不同频率的激振力,运动状态更为活跃的同时还有助于降低筛网堵塞概率。文章通过分析动力学模型的能量转换过程,利用拉格朗日公式推导出振动系统的运动微分方程;将等效滑模控制算法与主从控制结构相结合,实现稳定的双频控制同步运动;利用交流电机数学模型得到各电机的输出转矩和负载转矩方程,进而分别对两电机控制系统选择合适的滑模函数,设计出主电机速度追踪控制器和从电机相位追踪控制器的控制律表达式;引入饱和函数替换滑模控制器中的符号函数,以提升控制器的运行精度并降低变量在趋近过程中的抖振幅度,从理论角度明确所设计的电机控制器满足Lyapunov稳定性判据。同时,构建主从式双电机机电耦合双频同步控制模型,通过预设振动系统不同的控制条件以对控制理论的可行性和鲁棒性进行了深入分析。
Abstract:Aiming at the problem of slurry overflow caused by the inherent dynamic characteristics of traditional self-synchronous vibration screen in petroleum engineering, a novel controlled synchronous vibration system driven with double-frequency and dual-rotor is proposed, which can guarantee that the materials on screen mesh are subjected to the different excitation frequencies in a single cycle, and the motion state is more active to reduce the probability of screen mesh blocking. Firstly, in this paper, analyzing the energy conversion process of dynamical model, the motion differential equation of vibration system is derived by applying Lagrange’s formula. Secondly, equivalent sliding mode control algorithm is combined with the master-slave control structure to realize the stable dual-frequency control synchronization motion. Meanwhile, the output torque equation and the load torque equation of each motor are obtained by using mathematical model of AC motor. Subsequently, the suitable sliding mode functions are selected for the two motor control systems, and the control law expressions of velocity tracking controller and phase tracking controller are designed in detail. Then, the saturation function is introduced to replace the sign function in the sliding mode controllers, which can improve the operation accuracy of controller and reduce the chattering amplitude of the control variable during the process of approaching. Finally, according to the proposed control strategy, an electromechanical coupling synchronization control model with dual-motor and double-frequency actuation is constructed. Furthermore, feasibility and robustness of the control theory are verified by presetting different control conditions of the vibration system.
-
Keywords:
- vibration system /
- rotor dynamics /
- controlled synchronization /
- stability /
- double-frequency
-
振动筛系统除了可以应用在油气钻井行业,还因其普遍适用的振动同步原理广泛应用于冶金、化工、煤矿、交通等各个行业,俨然已成为国家经济持续发展的关键机械装备[1 − 3]。相应的振动同步理论也吸引了国内外大量研究者分别通过理论分析、数值计算、仿真模拟以及实验测试等方法对其展开一系列研究,这对振动机械的发明和发展具有重要的指导意义和促进作用。
国外关于2台振动电机之间的同步特性研究,最先是由Blekhman[4]利用直接运动分离法从数学理论上证明了振动系统中双激振器存在自同步振动以及满足自同步稳定性的条件,同时系统地介绍了不同力学模型的振动系统非线性动力学效应、一般方法与应用。随后,Paz等[5]结合振动工程需求进一步阐述了振动机械在物料输送方面的应用前景,从环保角度出发,采用结构力学中的刚度法对振动设备设计要点进行讨论和分析,提出了一种空间任意安装位置的双转子机械系统,并应用Hamilton原理解释了系统自同步相位角存在2个解,其中只有一个解具有稳定条件。Slepyan等[6]提出一种在参数共振模式下工作的振动筛系统,成功将振动响应求解问题简化为2个非线性耦合的常微分方程,并通过数值解析方法精确找到系统参数与振幅间的映射关系。国内关于振动机械的同步理论由闻邦椿院士创造性地提出,闻院士利用积分平均思想揭示了多个相同激振电机在超远共振条件下的同步特性和动力学响应,深入阐述了机械振动系统同步理论的应用与发展需求[7]。针对由机电耦合诱导的单频振动系统同步传动行为,侯勇俊等[8]利用转子动力学理论成功构造双转子直线−椭圆双轨迹振动系统的优化设计模型, 揭示了转子与振动质体间同步传动的机电耦合机制,并结合工程实际设计了一款由多机激励的平动椭圆振动筛。与上述学者提出的模型不同,文献[9 − 11]根据2个同频激振器激励双质体振动系统动力学模型,进一步揭示了系统中存在的Sommerfeld 效应,并通过建立机电耦合模型,给出了转速和振动在谐振点处的跳变现象。而关于振动系统双频同步理论研究,目前也有部分学者对其进行了试探性讨论。Modrzewski等 [12]从矿料废弃物回收利用的角度出发,通过不同激振类型的振动筛筛分实验发现,由多种激励频率驱动的振动系统物料筛分效率确实优于其他同频驱动振动系统,但是此研究缺乏相应的理论分析。姚运仕等[13]从沥青混合料筛分角度出发,设计了一种由电机驱动齿轮系的多频强迫同步合成振动筛,利用正交试验手段讨论了双频合成振动筛对于物料筛分具有较好的优越性,但强迫同步的驱动方式大大增加了结构装置疲劳失效的发生概率,同时减少整个振动系统的使用寿命。
近年来随着多电机同步控制结构的全面发展,关于同步控制算法的理论研究也相应地取得巨大进步。赵春雨等[14]通过设计非线性系统隶属度函数和模糊控制器,获得激振电机的转子速度、定子和转子电阻、瞬时外负载等辨识结果并确定其转矩电流,实现了两激振器的无速度传感器控制。文献[15 − 16]推导了锐共振振动系统中模糊自适应控制模型的控制律,并在感应电机矢量控制模型中考虑有鲁棒项,使非线性系统同步振动时仍能有效抑制外部参数扰动的影响,为大处理量、高振幅型振动筛系统的研发提供了重要的理论参考。Jia等[17]和刘云山等[18]对转速比为非整数值时的双电机受控同步特性进行了初步研究,通过将主从控制和模糊PID控制理论联系在一起,推导出振动系统比例、积分和微分的参数方程,并利用MATLAB/Simulink仿真验证了双转子分数同步的可行性。文献 [19 − 21]将自适应滑模控制理论与主从控制结构相结合,设计了一种由同频电机驱动的复合同步筛分系统,在振动筛节能技术中具有重要的工程意义。黄志龙等[22]对矿石颗粒耦合且具有变负载转矩特征的超远共振系统,采用相邻交叉耦合控制策略揭示了同向旋转电机之间的机电耦合特性,并发现该非线性振动系统可以获得稳定的线性振动。
目前关于振动系统的自同步和控制同步理论研究主要侧重于单频激励多电机振动系统。对于双频驱动振动系统的动力学特性和控制同步行为并未全面揭示,系统同步稳定性影响尚不够清楚。因此,本文考虑到高频电机和低频电机内部存在电气参数差异,提出了双转子振动系统双频同步性控制策略,并研究出一种基于等效滑模算法的主从控制结构方案,以实现稳定的双频控制同步。
1. 力学模型及运动微分方程
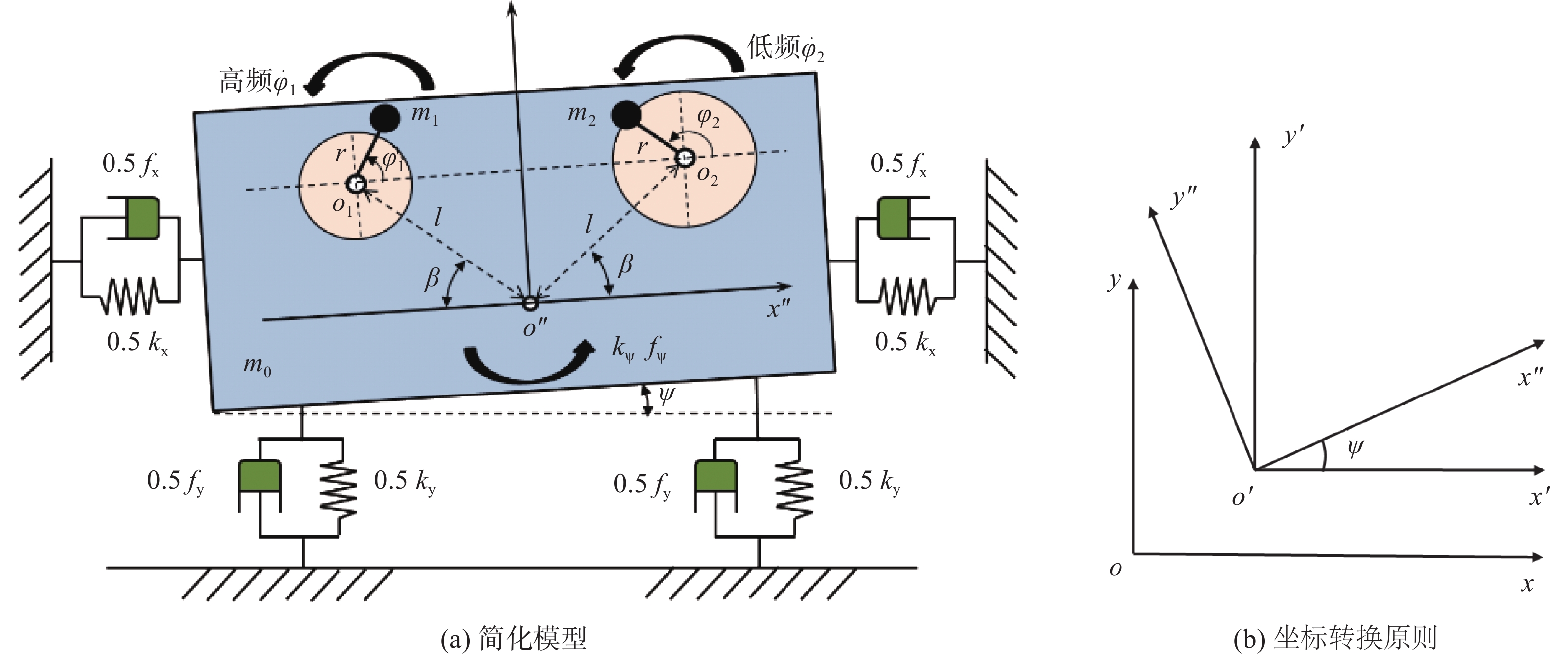
如图1所示建立远共振条件下双频驱动双转子振动系统的力学模型。2个同向旋转的激振电机对称且固定安装于质量m0的振动质体之上。由各激振电机驱动的偏心块等效为一质量为mi、偏心半径均为r的质点(i=1、2)。振动体由4根压缩弹簧支撑,在x、y、ψ方向分别考虑为刚度系数kx、 ky、 kψ和阻尼系数fx、 fy、 fψ 的弹性连接。以振动系统质心o″建立旋转坐标系x″o″y″,低频电机和高频电机的位置结构可由安装倾角β和激振电机到振动系统质心的距离l决定。令偏心转子i绕自身旋转中心oi转动的瞬时角位移为φi;箱体的瞬时摆动角位移为ψ。系统的参考坐标系如图1(b)所示,参考平面xoy为系统的固定坐标系,x′o′y′为系统的位移坐标系,x″o″y″为系统的旋转坐标系。可以看出,双频驱动双转子振动系统共有5个自由度,包括在x、y方向上的平动位移,ψ方向上的振动质体摆动位移以及2个偏心转子的旋转角。由于激振电机激励的偏心转子均在x″o″y″平面内运动,沿该平面的垂直方向并无其他激振力,因此,该振动系统视为一个双机驱动双转子平面振动系统。
当系统位于初始状态时,振动系统的3个参考面相互重合,每个转子在参考面x″o″y″中的坐标Φi″(i=1, 2)分别为:
$$ \begin{split} & {{\boldsymbol{\varPhi}}}_1^{''}=\left[\begin{gathered}-l\; \cos\; \beta+r\; \cos\; \varphi_1 \\ l\; \sin\; \beta+r\; \sin\; \varphi_1 \\ \end{gathered}\right], \\ &{\boldsymbol{\varPhi}}_2^{''}=\left[\begin{gathered}l\; \cos\; \beta+r\; \cos\; \varphi_2 \\ l\; \sin\; \beta+r\; \sin\; \varphi_2 \\ \end{gathered}\right] \end{split} $$ (1) 根据平面运动坐标转换原则,关于Φi和Φi″的坐标矩阵转换方程表示为:
$$ \boldsymbol{\boldsymbol{\varPhi}}_i=\left[\begin{gathered}x \\ y \\ \end{gathered}\right]+\boldsymbol{\boldsymbol{K}\boldsymbol{\varPhi}}_i^{''},\text{ }\boldsymbol{\boldsymbol{{K}}}=\left[\begin{gathered}\; \cos\; \psi\text{ }-\sin\; \psi \\ \; \sin\; \psi\text{ }\; \cos\; \psi \\ \end{gathered}\right]\text{, }i\text{ = 1,2} $$ (2) 式中:Φi 为第i个转子的固定坐标矩阵;[x y]T 为系统质心沿x、y幅值矩阵;K为变换矩阵。根据式(1)和式(2),获得各转子在平面xoy内的固定坐标,为:
$$\begin{split} & {{\boldsymbol{\varPhi }}_1} = \left[ {\begin{array}{*{20}{c}} {x - l\;\cos\; (\beta - \psi ) + r\;\cos\; ({\varphi _1} + \psi )} \\ {y + l\;\sin\; (\beta - \psi ) + r\;\sin\; ({\varphi _1} + \psi )} \end{array}} \right],\\ &{{\boldsymbol{\varPhi }}_2} = \left[ {\begin{array}{*{20}{c}} {x + l\;\cos\; (\beta + \psi ) + r\;\cos\; ({\varphi _2} + \psi )} \\ {y + l\;\sin\; (\beta + \psi ) + r\;\sin\; ({\varphi _2} + \psi )} \end{array}} \right] \end{split}$$ (3) 结合振动力学基本原理,箱体和每个转子在运转过程中产生的总动能E、总势能U以及总耗散能D可以描述为:
$$ \begin{split} &\begin{gathered} \begin{array}{c} E = \dfrac{1}{2}{m_0}{{\dot x}^2} + \dfrac{1}{2}{m_0}{{\dot y}^2} + \dfrac{1}{2}{J_m}{{\dot \psi }^2} + \dfrac{1}{2}\sum\limits_{i = 1}^2 {{J_i}{{\dot \varphi }_i}^2} +\\ \dfrac{1}{2}\sum\limits_{i = 1}^2 {{m_i}{\mathbf{\dot \varPhi }}_i^{\text{T}}{{{\mathbf{\dot \varPhi }}}_i}} \\ U = \dfrac{1}{2}{k_x}{x^2} + \dfrac{1}{2}{k_y}{y^2} + \dfrac{1}{2}{k_\psi }{\psi ^2} \\ D = \dfrac{1}{2}{f_x}{{\dot x}^2} + \dfrac{1}{2}{f_y}{{\dot y}^2} + \dfrac{1}{2}{f_\psi }{{\dot \psi }^2} + \dfrac{1}{2}{f_1}{{\dot \varphi }_1}^2 + \dfrac{1}{2}{f_2}{{\dot \varphi }_2}^2 \end{array} \end{gathered}\\[-16pt]& \end{split}$$ (4) 式中:Ji = mir2;Jm 为箱体的转动惯量;Ji为第i个偏心块的转动惯量;fi 为电机轴i的摩擦阻尼系数。最后根据分析力学中各质点系受到非有势力Q作用的保守系统,拉格朗日公式具有一般形式,为
$$ \dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\partial E}{\partial\boldsymbol{\dot{q}}}\right)-\dfrac{\partial(E-U)}{\partial\boldsymbol{\boldsymbol{q}}}+\dfrac{\partial D}{\partial\boldsymbol{\dot{q}}}=\boldsymbol{Q} $$ (5) 式中:q为系统的广义坐标矩阵,q=[x, y, ψ, φ1,φ2];${\boldsymbol{\dot q}}$为系统的速度矩阵,$ {\boldsymbol{\dot q}} = [\dot x,\dot y,\dot \psi ,{\dot \varphi _1},{\dot \varphi _2}] $;Q为系统的广义力矩阵,Q=[Qx, Qy, Qψ, Qφ1, Qφ2]。整个装置只会受到由电机产生的电磁转矩$ {M_{ei}} - {R_{ei}} $,可将各自由度的广义力矩阵分别考虑为:
$$ {\text{[}}{Q_x}{\text{, }}{Q_y}{\text{, }}{Q_\psi }{\text{, }}{Q_{\varphi 1}}{\text{, }}{Q_{\varphi 2}}{\text{]}} = {\text{[}}0{\text{, }}0{\text{, }}0{\text{, }}{M_{e1}} - {R_{e1}}{\text{, }}{M_{e2}} - {R_{e2}}{\text{]}} $$ (6) 结合实际工程,系统的不平衡转子质量相比于振动质体的质量非常小,即mi$ \ll $m0。同时质体的摆动位移远小于1 rad。忽略由电机安装位置误差产生的微小耦合项,将双频激振器激励的振动系统视为一个多自由度平面驱动振动系统。根据拉格朗日公式(5)推导出动力学模型中箱体和每个转子的运动微分方程为:
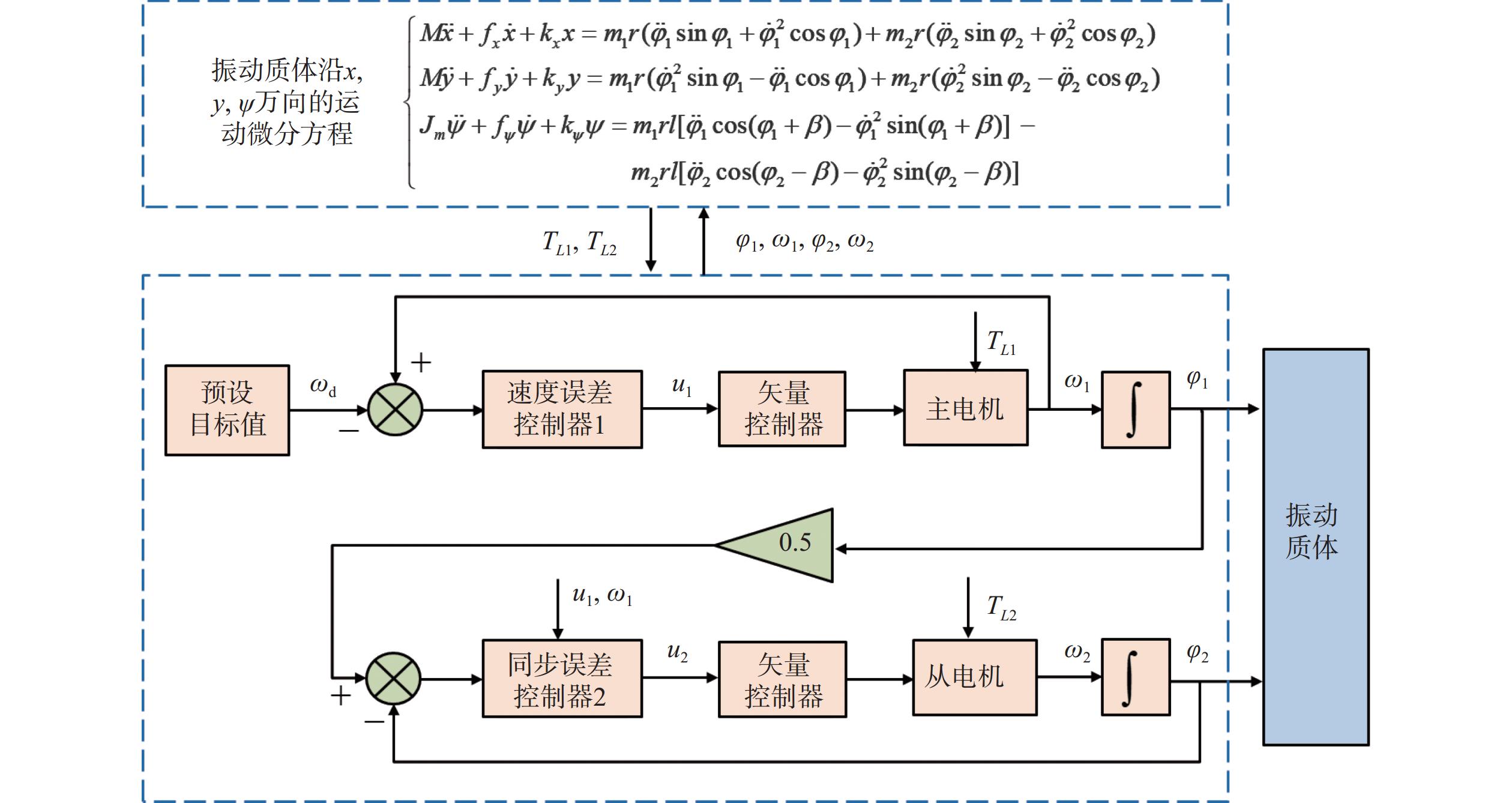
$$\begin{split} &\begin{gathered} \begin{array}{c} M\ddot x + {f_x}\dot x + {k_x}x = {m_1}r({{\ddot \varphi }_1}\;\sin\; {\varphi _1} + {{\dot \varphi }_1}^2\;\cos\; {\varphi _1}) + \\ {m_2}r({{\ddot \varphi }_2}\;\sin\; {\varphi _2} + {{\dot \varphi }_2}^2\;\cos\; {\varphi _2}) \\ M\ddot y + {f_y}\dot y + {k_y}y = {m_1}r({{\dot \varphi }_1}^2\;\sin\; {\varphi _1} - {{\ddot \varphi }_1}\;\cos\; {\varphi _1}) +\\ {m_2}r({{\dot \varphi }_2}^2\;\sin\; {\varphi _2} - {{\ddot \varphi }_2}\;\cos\; {\varphi _2}) \\ {J_m}\ddot \psi + {k_\psi }\psi + {f_\psi }\dot \psi = {m_1}rl[{{\ddot \varphi }_1}\;\cos\; ({\varphi _1} + \beta ) -{{\dot \varphi }_1}^2\;\sin\; ({\varphi _1} + \\ \beta )] - {m_2}rl[{{\ddot \varphi }_2}\;\cos\; ({\varphi _2} - \beta ) - {{\dot \varphi }_2}^2\;\sin\; ({\varphi _2} - \beta )] \\ {J_1}{{\ddot \varphi }_1} = {M_e}_1 - {f_1}{{\dot \varphi }_1} + {T_{L1}} \\ {J_2}{{\ddot \varphi }_2} = {M_e}_2 - {f_2}{{\dot \varphi }_2} + {T_{L2}} \end{array} \end{gathered}\\[-16pt]& \end{split} $$ (7) 式中:M = m0+m1+m2;Jm= m0le2;M 为系统总质量;le 为箱体绕质心的等效摆动半径。同时,电机的负载转矩TLi (i=1、2)可表示为:
$$ \begin{split} &\begin{gathered} \begin{array}{c} {T_{L1}} = {m_1}r[\ddot x\;\sin\; {\varphi _1} - \ddot y\;\cos\; {\varphi _1} + l\ddot \psi \;\cos\; ({\varphi _1} + \beta ) +\\ l{{\dot \psi }^2}\;\sin\; ({\varphi _1} + \beta )] \\ {T_{L2}} = {m_2}r[\ddot x\;\sin\; {\varphi _2} - \ddot y\;\cos\; {\varphi _2} - l\ddot \psi \;\cos\; ({\varphi _2} - \beta ) -\\ l{{\dot \psi }^2}\;\sin\; ({\varphi _2} - \beta )] \end{array} \end{gathered}\\[-16pt]& \end{split} $$ (8) 由于双频同步控制下的双转子振动系统内部存在多个变量耦合的特点,因此,需要分析电机与系统运动之间的关系。为了解决双频驱动振动系统的控制同步问题,有必要对每台振动电机的动态特性进行研究。根据式(7),将激振电机的三相绕组相对于d轴和q轴转换为两相系统,每个激振电机在转子磁链定向参考系下的磁链计算方法都可以用矩阵形式描述,为:
$$ \begin{split} & \left[ {\begin{array}{*{20}{c}} {{\psi _{d{\mathrm{s}}}}} \\ {{\psi _{d{\mathrm{r}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{L_{\mathrm{s}}}}&{{L_{\mathrm{m}}}} \\ {{L_{\mathrm{m}}}}&{{L_{\mathrm{r}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_{d{\mathrm{s}}}}} \\ {{i_{d{\mathrm{r}}}}} \end{array}} \right] \\ & \left[ {\begin{array}{*{20}{c}} {{\psi _{q{\mathrm{s}}}}} \\ {{\psi _{q{\mathrm{r}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{L_{\mathrm{s}}}}&{{L_{\mathrm{m}}}} \\ {{L_{\mathrm{m}}}}&{{L_{\mathrm{r}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_{q{\mathrm{s}}}}} \\ {{i_{q{\mathrm{r}}}}} \end{array}} \right] \end{split} $$ (9) 式中:ψdr、 ψqr分别为d、q方向上的转子磁链;ψds、ψqs分别为d、q方向上的定子磁链;Ls、Lr分别为定子电感和转子电感;Lm为定子和转子的互感系数;ids、iqs分别为d、q方向上的定子电流;idr、 iqr分别为d、q方向上的转子电流。另外,根据一般性电机控制原理[23],考虑振动电机的磁极对数为np,则每个电机的输出转矩方程Me可近似线性化为:
$$ \begin{split} & {M_e} = {K_T}{i_{q{\mathrm{s}}}} \\ & {K_T} = 3{n_p}{L_{\mathrm{m}}}{\psi _{d{\mathrm{r}}}}/{\text{(}}2{L_{\mathrm{r}}}{\text{)}} \end{split}$$ (10) 2. 系统滑模控制结构设计
振动系统的双频自同步状态(即相位差α=φ1−2φ2)主要由激振器安装在箱体上的位置结构、偏心质量大小等一系列系统参数确定,而且必须满足稳定性条件。也就是说,自同步振动系统在工程实际应用中具备固有的动态耦合特性,系统的同步状态不发生变化,通常不能灵活满足石油钻井工程的筛分作业要求。另外,由于高频激振电机和低频激振电机内部存在电气参数差异,因此,高频转子与低频转子若完全依靠自身电机特性时,并不能获得理想的二倍转速关系。要使双频同步振动筛系统具有预定的物料筛分功能,振动质体需要拥有稳定的幅值响应和同步运动状态,因此,有必要针对双机振动系统的倍频同步控制技术展开更深层次研究。
如图2所示,本文提出了一种基于滑模变结构控制算法的主从控制结构方案,以此实现高频转子与低频转子间的双频受控同步运动。整个控制系统主要包括主从控制结构、速度误差追踪控制器、相位同步误差控制器和矢量控制器等。设定高频振动电机1为系统主电机,低频振动电机2为系统从电机。鉴于滑模变结构控制算法具有高精度控制特点,可引入至系统的主电机和从电机控制器设计中,前者用于控制高频转子的旋转速度,后者用于控制低频转子的相位角。将主电机瞬时速度与系统预先设置的参考值之间的差值定义为控制器1的输入信号。此时,在确定主电机相位角增益为0.5的情况下,将其与从电机瞬时相位角之间的差值进一步定义为控制器2的输入信号。可以看出,振动系统的激振力由2个振动电机提供,从而影响振动质体的位移响应,反之,系统的振动响应也会影响电机的负载转矩的变化。采用图2所示的控制方案可以确保从电机瞬时相位角实时跟随主电机的运动情况以实现双频受控同步运动。
3. 各电机控制器数学理论
3.1 主电机速度追踪控制器
根据双频同步控制结构方案,首先需要设计主电机的速度误差控制律。考虑速度控制器1的信号误差为e1,即
$$ {e_1} = {\omega _1} - {\omega _{\mathrm{d}}} $$ (11) 式中:ω1 为主电机的实际转速;ωd 为整个系统预设的目标转速。将式(10)引入式(7)的电机1运动方程中,得到
$$ {J_1}{\ddot \varphi _1} = {K_{T1}}{u_{01}} - {f_1}{\dot \varphi _1} + {h_1} $$ (12) 其中
$$ \begin{split} & {h_1}{{ = }}{m_1}r[\ddot x\;\sin\; {\varphi _1} - \ddot y\;\cos\; {\varphi _1} + l\ddot \psi \;\cos\; ({\varphi _1} + \beta ) +\\ & \qquad\qquad \quad l{{\dot \psi }^2}\;\sin\; ({\varphi _1} + \beta )] \\ &\qquad\qquad\qquad {u_{01}}{{ = }}{i_{qs1}} \end{split} $$ (13) h1表示主电机内部存在的不确定项,其数值范围应小于或等于一个正实数,即h1是有边界的。同时,式(12)表明通过控制主电机输入电流u01可以控制电机的运动状态。此外根据式(11),对速度追踪误差e1求取一阶导数可得
$$ {\dot e_1} = {\dot \omega _1} - {\dot \omega _{\mathrm{d}}} $$ (14) 结合式(12)和式(14)并重新整理,$ {\dot e_1} $可表示为
$$ {\dot e_1} = {K_{T1}}{u_{01}}{\text{/}}{J_1} - {f_1}{\omega _1}{\text{/}}{J_1} + {h_1}{\text{/}}{J_1} - {\dot \omega _{\mathrm{d}}} $$ (15) 根据滑模变结构控制理论,选取速度追踪控制器的滑模函数类型为积分滑模函数s1,其滑模面设计为
$$ s_{\text{1}}=e_1-e_1\text{(0)}+c_1\int_0^te_1\text{(}\tau\text{)}\mathrm{d}\tau $$ (16) 式中:e1(0)为初始状态时的速度误差;c1为一个正实数。分析式(16)可知,当s1 = 0时,此方程存在收敛解,其结果为e1(t)= e1(0)${\mathrm{e}}^{c_1^t} $。即随着时间t逐渐趋近于无穷大时,速度追踪误差e1(t)逐渐收敛于零,其趋近速度是依赖于参数c1的取值。由此可得,控制器中积分滑模函数面s1的收敛状态实质上等价于速度追踪误差e1(t)的收敛状态。
本文在双频双电机控制同步振动系统的主电机控制器中引入了等效滑模控制方法。该控制方法设计较为简单,但振动信号的响应速度快,同时能够精确追踪到系统的目标值。主电机控制器中的滑模控制律主要包含等效控制项ueq1和切换鲁棒控制项usw1两部分。其中:等效控制项ueq1是用于确保振动系统的运动控制变量能够处于积分滑模函数面s1 = 0上;切换鲁棒控制项usw1则是保证振动系统的控制变量在积分滑模面上的稳定性,使其不偏离切换面。此时,考虑式(15)和式(16),$ {\dot s_{\text{1}}} $可以表示为
$$ {\dot s_{\text{1}}} = {K_{T1}}{u_{01}}{\text{/}}{J_1} - {f_1}{\omega _1}{\text{/}}{J_1} + {h_1}{\text{/}}{J_1} - {\dot \omega _d} + {c_1}{\text{(}}{\omega _1} - {\omega _{\mathrm{d}}}{\text{)}} $$ (17) 令$ {\dot s_{\text{1}}} = 0 $,并忽略外部不确定干扰量h1,主电机的等效控制项ueq1推导为
$$ u_{\mathrm{eq}1}=u_{01}=J_1\text{(}f_1\omega_1\text{/}J_1+\dot{\omega}_{\mathrm{d}}-c_1e_1\text{)/}K_{T1} $$ (18) 为了增强速度追踪控制器的稳定性,有效抑制因外部环境干扰引起的摄动量,切换鲁棒控制项usw1设计为
$$ u_{\mathrm{sw}1}=-J_1\chi_1\mathrm{sgn}\text{(}s_1\text{)/}K_{T1} $$ (19) 式(19)中χ1为系统的控制参数,χ1 > 0。sgn(s1)是符号函数,即
$$ {{\mathrm{sgn}}} {\text{(}}{s_1}{\text{) = }}\left\{ \begin{gathered} 1,{\text{ }}{s_1} > 0 \\ 0,{\text{ }}{s_1} = 0 \\ - 1,{\text{ }}{s_1} < 0 \\ \end{gathered} \right. $$ (20) 因此,根据式(18)和式(19),双频双电机控制同步振动系统中主电机速度误差控制器的滑模控制律表达式描述为
$$ \begin{split}u_1 & =u_{\mathrm{eq}1}+u_{\mathrm{sw}1}= \\ J_1\text{[}f_1\omega_1\text{/}J_1+&\dot{\omega}_{\mathrm{d}}-c_1e_1-\chi_1\mathrm{sgn}\text{(}s_1\text{)]/}K_{T1}\end{split} $$ (21) 在实际振动与控制工程中,理想且光滑的滑动模态并不存在。此外,在滑模变结构控制过程中,由于控制变量在时间上的滞后或者空间上的顿挫导致振动系统时常伴有“抖振”现象。于是,为削弱变量在趋近过程中的抖振幅度,引入饱和函数sat(s1)替换控制律(21)中的符号函数,即
$$ {{\mathrm{s}}} {\text{at(}}{s_1}{\text{) = }}\left\{ \begin{gathered} 1,{\text{ }}{s_1} > \Delta \\ \xi {s_1},{\text{ }}\left| {{s_1}} \right| \leqslant \Delta ,{\text{ }}\xi = 1/\Delta \\ - 1,{\text{ }}{s_1} < - \Delta \\ \end{gathered} \right. $$ (22) 式中:Δ 是边界层,可视为一个较小的正实数。使用sat(s1)实现双频同步控制的原因在于:在Δ外面可以考虑为切换控制方法,提升控制变量趋近至滑模面时的速度;在Δ内部则可以考虑为反馈控制方法,减小控制变量到达滑模面后因惯性产生的抖动。综上,主电机的最终速度追踪误差控制器设计形式为
$$ {u_1} = {J_1}{\text{[}}{f_1}{\omega _1}{\text{/}}{J_1} + {\dot \omega _{\mathrm{d}}} - {c_1}{e_1} - {\chi _1}{{\mathrm{s}}} {\text{at(}}{s_1}{\text{)]/}}{K_{T1}} $$ (23) Lyapunov稳定性准则普遍应用于对各种非线性运动控制系统以及广义离散时变系统等的稳定性研究。为此,本文利用此稳定性准则从理论上探明所设计的速度追踪误差控制律是否具有稳定性。设定Lyapunov函数为V1,即
$$ {V_1} = \dfrac{1}{2}s_1^2 $$ (24) 由式(24)可知,V1 = 0时, s1 = 0,且V1 > 0时, s1≠0,满足Lyapunov稳定性判据的前提。将主电机的滑模控制律(23)代入式(17),$ {\dot s_{\text{1}}} $可以重新写为
$$ {\dot s_1} = - {\chi _1}{\text{sgn(}}{s_1}{\text{)}} + {h_1}{\text{/}}{J_1} $$ (25) 对式(24)关于时间求导并考虑式(4)—(18),得到$ {\dot V_1} $,为
$$ \begin{split} & {{\dot V}_1} = {s_1}{{\dot s}_1} = {s_1}{\text{[}} - {\chi _1}{\text{sgn(}}{s_1}{\text{)}} + {h_1}{\text{/}}{J_1}{\text{]}}= - \\ & {\chi _1}\left| {{s_1}} \right| + {h_1}{s_1}{\text{/}}{J_1} \leqslant {\text{(}} - {\chi _1} + \left| {{h_1}} \right|{\text{/}}{J_1}{\text{)}}\left| {{s_1}} \right| \end{split} $$ (26) 显然,当χ1 > max ( |h1| / J1 ) = h1max / J1时,$ {\dot V_1} \leqslant 0 $。由此可知,主电机控制系统满足Lyapunov稳定性理论,即$\mathop {\lim }\limits_{t \to \infty } {s_1}(t) = 0$。此时,主电机的实际转速可以准确收敛至系统预设的目标值,其速度追踪误差控制器逐渐趋近于稳态。
3.2 从电机相位追踪控制器
根据振动系统的双频主从同步控制结构,设定主电机输出相位角φ1的增益为0.5,将其与从电机的瞬时相位角φ2之间的双频相位差作为相位同步控制器的控制变量,对从电机的相位进行实时追踪控制。因此,可以采用控制参数调节使其误差值收敛至零,并令从电机的相位同步误差为e2,即
$$ {e_2} = \dfrac{1}{2}{\varphi _1} - {\varphi _2} $$ (27) 同时,将式(10)引入式(7)的电机2运动方程中,可以重新写为
$$ {J_2}{\ddot \varphi _2} = {K_{T2}}{u_{02}} - {f_2}{\dot \varphi _2} + {h_2} $$ (28) 其中
$$ \begin{split} {h_2} = {m_2}r[\ddot x\;\sin\; &{\varphi _2} -\ddot y\;\cos\; {\varphi _2} - l\ddot \psi \;\cos\; ({\varphi _2} - \beta ) -\\ & l{{\dot \psi }^2}\;\sin\; ({\varphi _2} - \beta )] \\ &\quad {u_{02}}{\text{ = }}{i_{q{\mathrm{s}}2}} \end{split} $$ (29) h2表示主电机内部存在的不确定项,其数值范围应小于或等于一个正实数,即h2是有边界的。进一步,根据主从控制结构,将式(12)和式(28)相减,并考虑相位同步误差为e2,可以得到
$$ \begin{split} & {J_2}{{\ddot e}_2} + {f_2}{{\dot e}_2} = F - {\text{[(}}{J_1} - {J_2}{\text{/2)}}{{\ddot \varphi }_1} + {\text{(}}{f_1} - {f_2}{\text{/2)}}{{\dot \varphi }_1}{\text{]}} + H \\ &\qquad\qquad\qquad F{{ = }}{K_{T1}}{u_{01}} - {K_{T2}}{u_{02}} \\ &\qquad\qquad\qquad\quad H{{ = }}{h_1} - {h_2} \end{split} $$ (30) 与主电机速度误差控制器的设计类似,依然选取积分滑模函数s2作为从电机相位同步控制器的滑模面,为
$$ s_{\text{2}}=\dot{e}_2+c_2\int_0^te_2\text{(}\tau\text{)}\mathrm{d}\tau $$ (31) 令$ {\dot s_{\text{2}}} = 0 $,并忽略外部不确定干扰量H的影响,从电机的等效控制项ueq2推导为
$$ \begin{split} u_{\mathrm{eq}2}=u_{02}=&[K_{T1}u_{01}+J_2c_2e_2-f_2\dot{e}_2-\text{(}J_1-J_2\text{/2)}\ddot{\varphi}_1- \\ & \qquad\text{(}f_1-f_2\text{/2)}\dot{\varphi}_1]\text{/}K_{T2}\end{split} $$ (32) 为了实现对高频振动电机和低频振动电机之间的稳定双频同步控制,从电机的鲁棒性项设计为
$$ u_{\mathrm{sw}2}=J_2\chi_2\mathrm{sgn}\text{(}s_2\text{)/}K_{T2} $$ (33) 式中:χ2 为系统的控制参数,χ2 > 0。引入饱和函数sat(s2)至方程(32),则最终从电机相位同步误差控制器中的控制律表达式可设计为
$$ \begin{split} &\qquad \quad u_2 =u_{\mathrm{eq}2}+u_{\mathrm{sw}2}= \\ & [K_{T1}u_1+J_2c_2e_2-f_2\dot{e}_2-\text{(}J_1-J_2\text{/2)}\ddot{\varphi}_1- \\ & \quad\;\;\; \text{(}f_1-f_2\text{/2)}\dot{\varphi}_1+J_2\chi_2\mathrm{s}\text{at(}s_2\text{)}]\text{/}K_{T2} \end{split} $$ (34) 于是根据积分滑模函数s2定义的Lyapunov函数为:
$$ {V_2} = \dfrac{1}{2}s_2^2 $$ (35) 由此可知,V2 = 0时, s2 = 0, 且V2 > 0时, s2≠0,满足Lyapunov稳定性判据的前提。针对式(35)关于时间求导并考虑$ {\dot s_{\text{2}}} $,得到V2的导数为
$$\begin{split} {{\dot V}_{\text{2}}} &= {s_2}{{\dot s}_2} = {s_2}{\text{[}}H{\text{/}}{J_2} - {\chi _2}{\text{sgn(}}{s_2}{\text{)]}}= \\ & H{s_2}{\text{/}}{J_2} - {\chi _2}\left| {{s_2}} \right| \leqslant {\text{(}}\left| H \right|{\text{/}}{J_2} - {\chi _2}{\text{)}}\left| {{s_2}} \right| \end{split}$$ (36) 显然,当χ2 > max ( |H| / J2 ) = Hmax / J2时,$ {\dot V_2} \leqslant 0 $ 。从电机的瞬时相位可以准确追踪到主电机的输出相位角,从电机相位同步误差控制器逐渐趋近于稳态,从数学理论上证明了双频双电机控制同步振动系统中,将主从控制结构与滑模控制算法相结合的可行性和稳定性。
4. 机电耦合双频控制同步分析
为了论证3节中主从信号追踪控制器理论设计的准确性和可行性,本节将根据双转子振动系统微分动力学方程式(7)以及滑模控制律表达式(23)、式(34),通过MATLAB/Simulink模块建立双频同步控制下的机电耦合动力学模型,同时利用四阶Runge-Kutta 算法以实现振动系统动态特性的模拟计算。值得说明的是,在系统非同步状态下,摩擦力矩的数学模型是非线性的、不确定的,而在同步状态下,单周期内的平均摩擦力矩近似等于一个常数。因此,在仿真模型中,各电机轴的摩擦力矩将以0.005 Nms左右的小摩擦因数反映。系统的基本仿真参数如表1所示。
表 1 振动系统结构参数Table 1. Structural parameters of vibration system偏心转子 箱体 振动电机1 振动电机2 m1=1 kg m0=100 kg P1=0.12 kW P2=0.12 kW m2=1.5 kg kx= 75200 N/mUs=380 V Us=380 V r=0.05 m ky= 75200 N/mωs=50 Hz ωs=50 Hz l=0.4, 0.5 m kψ= 9550 N·m/radωm1=314 rad/s ωm=157 rad/s β=45°, 60° fx=185 N·s/m np1=1 np2=2 — fy=185 N·s/m Rs1=0.012 Ω Rs2=0.099 Ω — fψ=122 N·m·s/rad Rr1=0.01 Ω Rr2=0.058 Ω — Jm=10 kg·m2 Ls1=0.008 H Ls2=0.032 H — — Lr1=0.008 H Lr2=0.032 H — — Lm1=0.015 H Lm2=0.03 H 4.1 双频振动同步运动特性
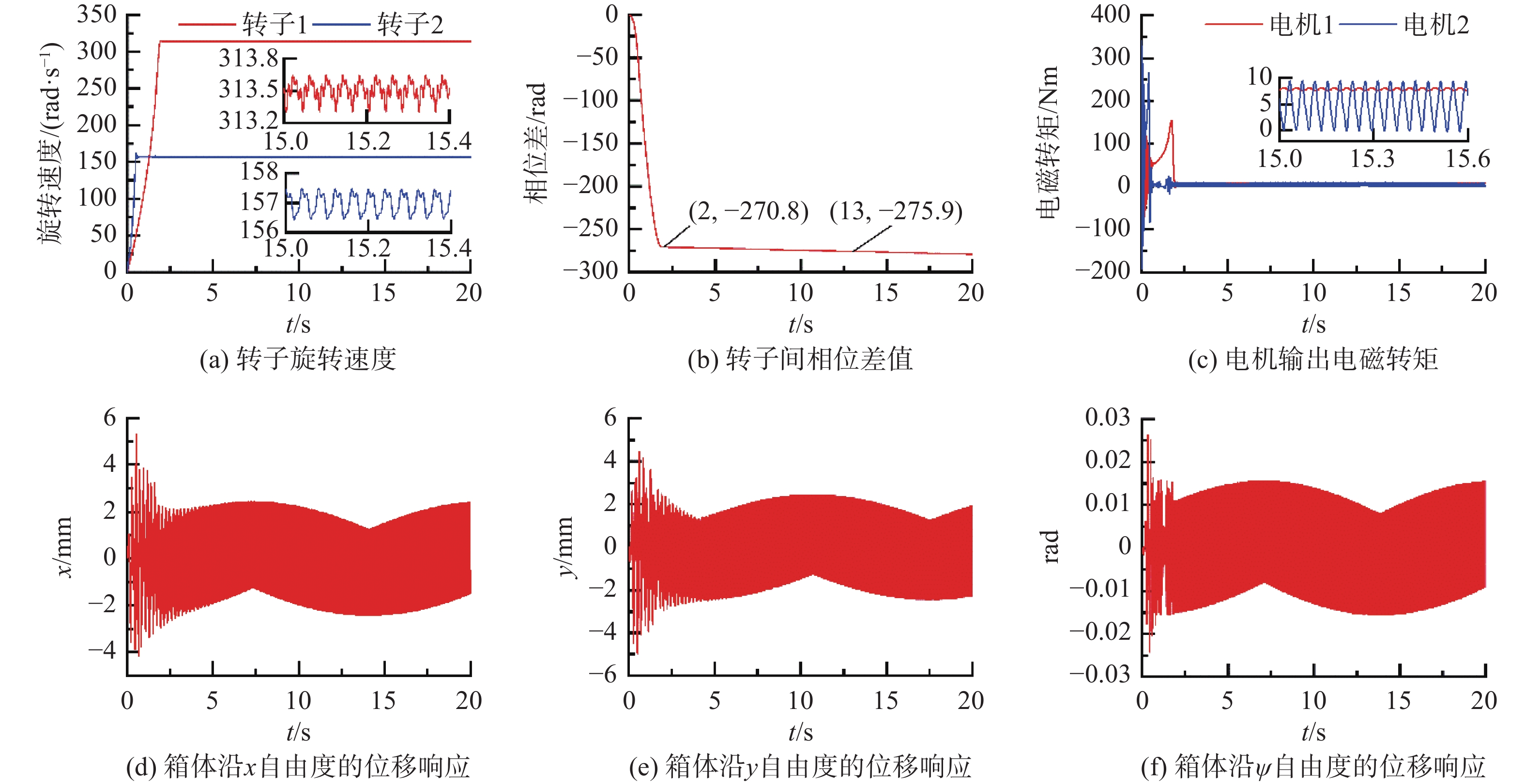
为与双频双转子控制同步效果形成一个明显的对比,本节首先研究机电耦合动力学模型在双频振动同步状态下的运动特性。设定系统参数β=45°、l=0.5 m,其他仿真参数与表1一致,计算结果如图3所示。直接启动2个振动电机的电源,使整个振动系统完全依靠内部自身的机电耦合特性产生振动同步运动。可以看出,低频转子在电机2的驱动下率先以157 rad/s的转速到达稳定运行状态,经过大约2 s后,高频转子转速在电机1的激励下以313.5 rad/s形成稳定波动。此时,若考虑高频转子和低频转子的瞬态相位角分别为φ1=313.5t+α1,φ2=157t+α2,得到振动系统的双频相位差值(α=φ1−2φ2=−0.5t+α1−2α2)不等于常数,为一个与时间t相关的变化量。因此,如图3(b)所示,转子之间的双频振动同步状态将以一个较小的斜率随时间逐渐降低,这是由于2台振动电机的转速关系没有按照固定的2倍比值运行造成的。由此可知,高频转子的瞬时相位角滞后于2倍的低频转子的瞬时相位角,该振动系统不能实现给定且稳定的双频振动同步运动。当各转子在机电耦合作用下从最初的启动阶段至短暂共振状态,最终到达各自额定转速后,2个振动电机的输出转矩分别在8 Nm和5 Nm附近波动,其波动状态的稳定性几乎不受转子速度比误差的影响,如图3(c)所示。图3(d)至(f)分别描述了系统振动质体沿c (c=x、y、ψ)自由度上的振幅响应情况。由于高频振动电机和低频振动电机各自以额定转速做周期性回转运动,所以振动质体在c方向上的幅值发生周期性的抵消和叠加。同时振幅响应的波峰值和波谷值因速度误差的存在导致相位角φ1和2φ2之间存在滞后和超前现象,从而出现非正余弦曲线的变化趋势,进一步证明了转子速度比误差的存在和双频相位差的不稳定性对整个振动系统动态响应的影响。综上所述,若系统完全依靠自身电机特性运行时,因内部电气参数差异造成速度比误差的存在并不能获得理想的2倍转速关系,导致振动系统的同步状态失稳。同时,转子间的双频相位差值因受限于振动同步的动力学固有属性而无法改变,抑制了工程中对振动机械运动特性多样性的要求。因此,如果不能保证高频振动电机和低频振动电机之间达到所需的转速比关系,由双频驱动转子之间的振动同步运动就无法适用于钻井液筛分工程中。
4.2 双频控制同步可行性验证
根据双频同步控制结构设计方案和振动系统机电耦合同步控制模型,本节将对主从电机控制器有效性以及双频同步特性曲线变化规律进行讨论,如图4所示。在进行控制同步计算仿真之前,预设系统的转速目标值ωd=314 rad/s,转子间的目标相位差为0 rad,高频转子的速度增益取0.5,系统相关控制参数c1=c2=200,χ1=χ2=200。此外,kp1= kp2=298.6, kc1= kc2=
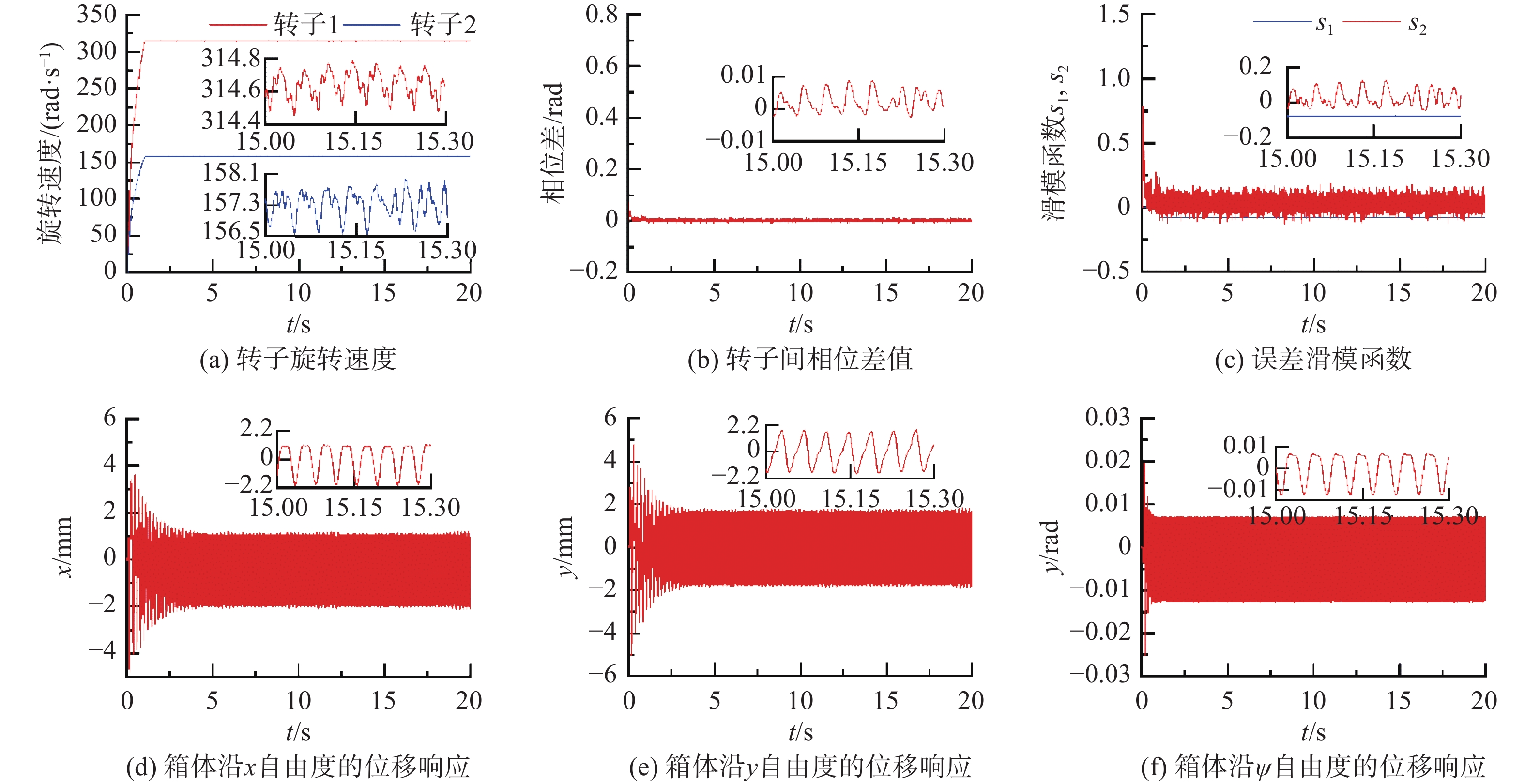
10875 ,其中kpi,kci (i=1,2)分别表示矢量控制系统中PI控制器的比例增益系数和积分增益系数,其他结构参数参照3节内容。如图4(a)所示,相比于双频振动同步状态下的振动系统,高频转子和低频转子在滑模控制算法作用下可以更快速到达指定目标转速314 rad/s和157 rad/s附近。当两振动电机同步工作时,速度值波动幅度分别为0.4 rad/s和1.6 rad/s,两者转速基本保持稳定。图4(b)表明振动系统的双频相位差在电源启动时由于短暂的共振影响而造成微弱波动后,将非常迅速地收敛至目标值0 rad附近,然而图3中的振动同步运动并不能获得同等效果,这明显表现出本文所提控制方法的优越性。高频转子与低频转子到达稳定同步状态后的转速比值一直锁定至2,即${\dot \varphi _{\text{1}}}{\text{ = 2}}{\dot \varphi _{\text{2}}}$,证明了双转子速度严格保持二倍关系是实现振动系统双频同步运动的前提条件。另外,主从电机在实现受控同步运动过程中的滑模函数s1、s2变化曲线如图4(c)所示,符合3节控制器理论设计要求。随着仿真时间增加,主电机的速度误差信号和从电机的同步误差信号均能逐渐收敛于零,其实质是保证了整个控制器中运动控制变量都可以处于积分滑模函数面si = 0 (i=1、2)上。通过合理选择控制参数ci和χi的值,使变量以一定趋近速度到达滑模面后并不会产生较大的运动偏移现象,实现对双频同步状态的有效控制。另一方面,高频转子和低频转子不仅需要拥有稳定的双频相位差值,同时振动体在周期性振动过程中还应具备稳定的位移响应曲线。图4(d)至(f)表示质体沿水平方向、竖直方向和摆动方向上的振幅,单侧分别为1 mm、1.2 mm以及0.008 rad。因此,与传统同频振动系统比较,基于控制同步方法的双频同步振动系统,可以作为满足振动机械工作要求的一种方案。4.3 控制同步鲁棒性验证
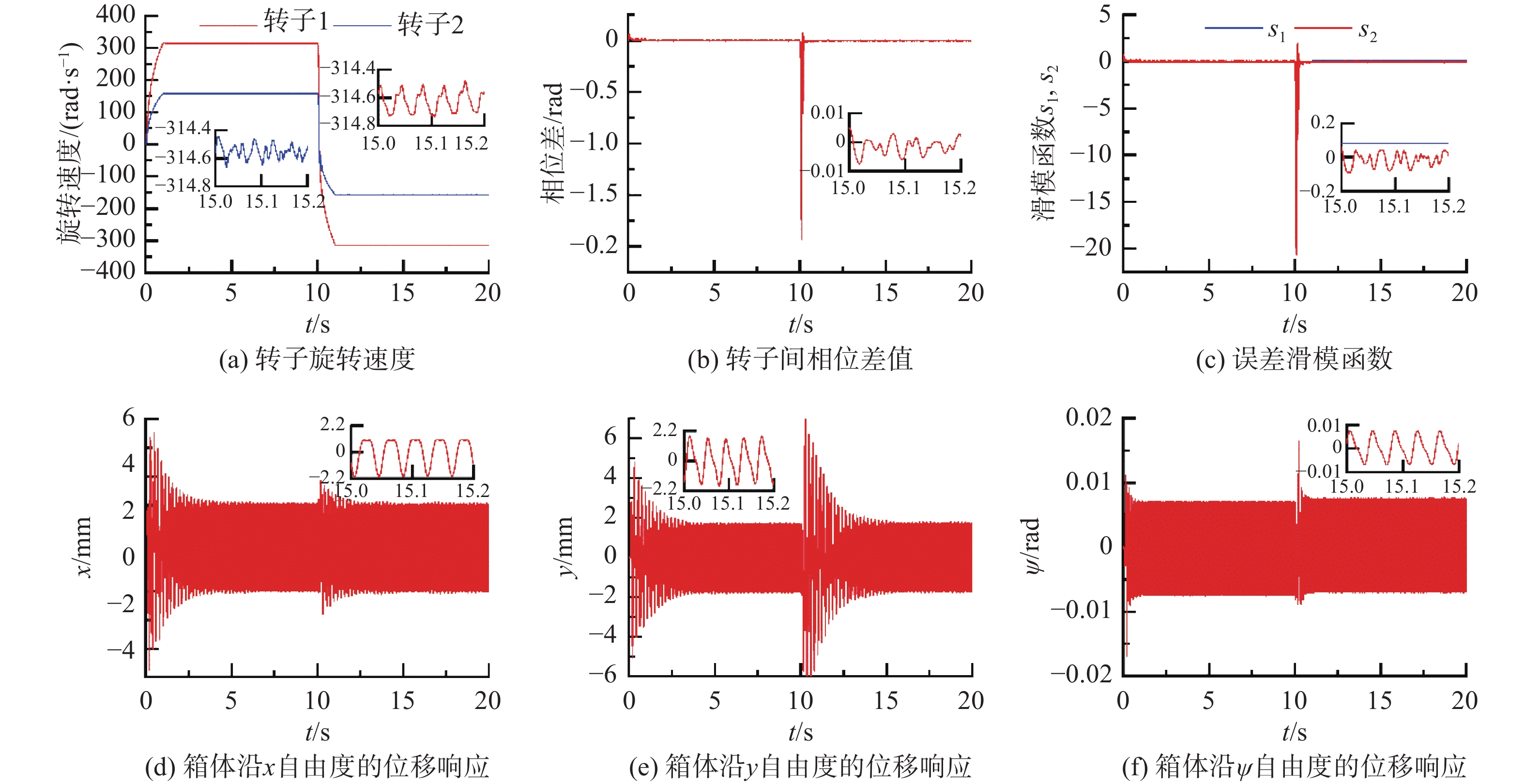
在工程应用中,时常需要通过调整参考速度值以获得振动系统的不同运行状态。同时,振动电机的安装误差和箱体的制造误差在机械加工过程中也是不可避免的。因此,本节将通过分析目标转速ωd突变、安装倾角β和安装距离l的变化带给控制系统的干扰,来验证控制系统是否具备鲁棒性并抵抗参数变化带来的影响。重新设定参数β=60°,l=0.4 m,ωd在系统运行至10 s时从314 rad/s突变至−314 rad/s,其他参数不变,最终受控同步结果如图5所示。在图5(a)中,直接同时启动的高低频振动电机的转速值能在1 s内快速接近目标值。当系统稳定运行至第10 s,目标转速接收控制指令后发生突变,高频电机和低频电机的转速可在短时间内分别调整至−314 rad/s和−157 rad/s附近,波动幅度约为0.2 rad/s和0.7 rad/s。如图5(b)所示:运行时间为前10 s时,双频相位差值一直维持在0 rad,表明在考虑主从控制结构和滑模控制算法的情况下,振动系统的同步状态不会因为安装倾角β和安装距离l的变化而出现不同步的现象;随后,当系统执行速度突变命令后,两转子的相位差立即发生波动。但是由于控制器中鲁棒控制项的引入,以及电机与振动质体间的机电耦合作用下,促使同步状态不被外界环境所干扰并再次锁定到目标值。图5(c)描述了式(23)主电机滑模函数和式(34)从电机滑模函数选择的正确性。通过在控制律表达式中将等效控制项和切换鲁棒控制项相结合,保证了速度误差信号和同步误差信号到达积分滑模面后的稳定性。图5(d)至(f)分别表示系统在x、y和ψ自由度上的位移响应。可以看出,各方向上的振幅在目标速度和结构参数变化的前提下仍能很快达到稳定状态。不同于同频振动同步运动,它们不再是标准的正余弦曲线,而是由2个不同振动频率波互相叠加的结果。综合以上分析可知,振动系统前10 s的运动特性论证了转子的同步性不会因结构参数改变而发生变化,后10 s揭示了控制器具备较强的鲁棒性,并可以明显抑制因转速改变对振动系统形成的影响。
5. 结论
由于系统固有的动态耦合特性,振动同步运动状态具有不变性和局限性,无法获得双频驱动振动系统的预定筛分功能。因此,针对高频振动电机和低频振动电机对称分布的双频振动系统,将控制理论和动力学理论联系在一起,进一步探究其控制同步机制。引入滑模变结构控制算法并与主从控制结构相结合,设计了关于偏心转子速度误差控制器以及同步误差控制器以优化自同步振动系统。现将本文结论概括如下。
1)根据双频同步控制下的对称分布双转子振动系统运动微分方程,利用交流电机三相绕组转化为两相系统的一般性控制原理获得了电机电磁转矩和负载转矩表达式。
2)详细阐述了振动系统完全依靠自身电机特性运行时,因速度比误差的存在并不能获得理想的二倍转速关系,转子间的双频振动同步状态将以一个较小的斜率随时间逐渐降低,导致振动系统的同步状态失稳。
3)系统地构建了双频激励双转子的控制方案,同时设计了合理的等效控制项和切换鲁棒项进而推导出速度和同步误差控制律表达式。引入饱和函数替换滑模控制器中的符号函数,以提升控制器的运行精度并降低变量在趋近过程中的抖振幅度。
4)通过建立机电耦合双频同步控制模型,论证了所提出的控制理论可成功实现双频驱动振动系统的受控同步运动。通过对比控制同步与振动同步的动态特性,发现同步性能参数均可得到稳定控制,如各转子速度、双频相位差以及箱体的位移响应等。此外,整个电机控制系统具备比较好的鲁棒性,可以不受参考速度改变、电机安装倾角和安装距离误差等内部或外界的扰动影响。
-
表 1 振动系统结构参数
Table 1 Structural parameters of vibration system
偏心转子 箱体 振动电机1 振动电机2 m1=1 kg m0=100 kg P1=0.12 kW P2=0.12 kW m2=1.5 kg kx= 75200 N/mUs=380 V Us=380 V r=0.05 m ky= 75200 N/mωs=50 Hz ωs=50 Hz l=0.4, 0.5 m kψ= 9550 N·m/radωm1=314 rad/s ωm=157 rad/s β=45°, 60° fx=185 N·s/m np1=1 np2=2 — fy=185 N·s/m Rs1=0.012 Ω Rs2=0.099 Ω — fψ=122 N·m·s/rad Rr1=0.01 Ω Rr2=0.058 Ω — Jm=10 kg·m2 Ls1=0.008 H Ls2=0.032 H — — Lr1=0.008 H Lr2=0.032 H — — Lm1=0.015 H Lm2=0.03 H -
[1] 李振民, 张学良, 岳红亮, 等. 双机驱动双质体振动机械系统的同步及其稳定性[J]. 振动与冲击, 2022, 41(4): 29 − 35. LI Z M, ZHANG X L, YUE H L, et al. Synchronization and stability of a vibrating mechanical system with double rigid frames driven by two vibrators[J]. Journal of Vibration and Shock, 2022, 41(4): 29 − 35.
[2] KUMAR D, WORKU Z A, GAO Y, et al. Comparison of wet milling and dry milling routes for ibuprofen pharmaceutical crystals and their impact on pharmaceutical and biopharmaceutical properties[J]. Powder Technology, 2018, 330: 228 − 238. doi: 10.1016/j.powtec.2018.02.022
[3] 张文宇, 陈晓哲. 翻车机振打装置的两机振动同步理论[J]. 矿山机械, 2023, 51(10): 18 − 22. doi: 10.3969/j.issn.1001-3954.2023.10.004 ZHANG W Y, CHEN X Z. Theory on vibration synchronization of two eccentric rotors in car dumper vibration device[J]. Mining & Processing Equipment, 2023, 51(10): 18 − 22. doi: 10.3969/j.issn.1001-3954.2023.10.004
[4] BLEKHMAN I I. Vibrational Mechanics[M]. Singapore: World Scientific, 2000.
[5] PAZ M, COLE J D. Self-synchronization of two unbalanced rotors[J]. Journal of Vibration and Acoustics, 1992, 114(1): 37 − 41. doi: 10.1115/1.2930230
[6] SLEPYAN L I, SLEPYAN V I. Coupled mode parametric resonance in a vibrating screen model[J]. Mechanical Systems and Signal Processing, 2014, 43(1-2): 295 − 304. doi: 10.1016/j.ymssp.2013.10.001
[7] 闻邦椿, 刘树英, 陈照波, 等. 机械振动理论及应用[M]. 北京: 高等教育出版社, 2009. WEN B C, LIU S Y, CHEN Z B, et al. Theory of mechanical vibration and its applications[M]. Beijing: Higher Education Press, 2009.
[8] 侯勇俊, 郭馨悦, 方潘, 等. 双电机双轨迹振动筛优化设计[J]. 机械设计与制造, 2022(10): 257 − 261. doi: 10.3969/j.issn.1001-3997.2022.10.056 HOU Y J, GUO X Y, FANG P, et al. Optimization design of the double-track vibrating screen with double exciting motors[J]. Machinery Design & Manufacture, 2022(10): 257 − 261. doi: 10.3969/j.issn.1001-3997.2022.10.056
[9] ZHANG X L, LI Z M, LI M, et al. Stability and sommerfeld effect of a vibrating system with two vibrators driven separately by induction motors[J]. IEEE/ASME Transactions on Mechatronics, 2021, 26(2): 807 − 817. doi: 10.1109/TMECH.2020.3003029
[10] 张学良. 双机及多机驱动振动系统同步理论的研究[D]. 沈阳: 东北大学, 2014. ZHANG X L. Study on synchronization theory of dual-machine and multi-machine driven vibration system[D]. Shenyang: Northeastern University, 2014.
[11] ZHANG X L, GU D W, YUE H L, et al. Synchronization and stability of a far-resonant vibrating system with three rollers driven by two vibrators[J]. Applied Mathematical Modelling, 2021, 91: 261 − 279. doi: 10.1016/j.apm.2020.07.047
[12] MODRZEWSKI R, WODZINSKI P. Screens for segregation of mineral waste[J]. Physicochemical Problems of Mineral Processing, 2011, 47: 267 − 74.
[13] 姚运仕, 李彦伟, 石鑫, 等. 双频合成振动压路机的工业化试验[J]. 长安大学学报(自然科学版), 2013, 33(2): 101 − 106. YAO Y S, LI Y W, SHI X, et al. Industrial experiment on double-frequency composed vibratory roller[J]. Journal of Chang'an University (Natural Science Edition), 2013, 33(2): 101 − 106.
[14] 赵春雨, 王得刚, 张昊, 等. 同向回转双机驱动振动系统的频率俘获[J]. 应用力学学报, 2009, 26(2): 283 − 287. ZHAO C Y, WANG D G, ZHANG H, et al. Frequency capture of vibration system with two-motor drives rotating in same direction[J]. Chinese Journal of Applied Mechanics, 2009, 26(2): 283 − 287.
[15] LI X, LIU J, LIU J. Analysis of the sharp resonance control synchronization for dual motors exciting nonlinear system based on sliding mode[J]. Applied Mechanics and Materials, 2009, 16-19: 352 − 357. doi: 10.4028/www.scientific.net/AMM.16-19.352
[16] 李小号. 非线性振动系统锐共振振动同步与控制同步关键技术研究[D]. 沈阳: 东北大学, 2010. LI X H. Research on key technologies of sharp resonance vibration synchronization and control synchronization of nonlinear vibration system[D]. Shenyang: Northeastern University, 2010.
[17] JIA L, KONG X X, ZHANG J Q, et al. Multiple-frequency controlled synchronization of two homodromy eccentric rotors in a vibratory system[J]. Shock and Vibration, 2018, 2018(1): 4941357. doi: 10.1155/2018/4941357
[18] 刘云山, 贾磊, 闻邦椿. 反向回转双机驱动振动系统的倍频控制同步[J]. 东北大学学报(自然科学版), 2019, 40(12): 1726 − 1731. doi: 10.12068/j.issn.1005-3026.2019.12.011 LIU Y S, JIA L, WEN B C. Multi-frequency controlled synchronization of a vibrating system with two-motor drives rotating in opposite directions[J]. Journal of Northeastern University (Natural Science), 2019, 40(12): 1726 − 1731. doi: 10.12068/j.issn.1005-3026.2019.12.011
[19] 孔祥希. 多机驱动振动系统的控制同步与复合同步理论研究[D]. 沈阳: 东北大学, 2016. KONG X X. Controlled and composite synchronizations in the vibrating system driven by multi-motors[D]. Shenyang: Northeastern University, 2016.
[20] KONG X X, ZHOU C, WEN B C. Composite synchronization of four exciters driven by induction motors in a vibration system[J]. Meccanica, 2020, 55(11): 2107 − 2133. doi: 10.1007/s11012-020-01246-7
[21] KONG X X, JIANG J, ZHOU C, et al. Sommerfeld effect and synchronization analysis in a simply supported beam system excited by two non-ideal induction motors[J]. Nonlinear Dynamics, 2020, 100(3): 2047 − 2070. doi: 10.1007/s11071-020-05626-2
[22] 黄志龙, 张众超, 楚树坡, 等. 四激振器激励下振动机械-物料系统同步控制[J]. 振动 测试与诊断, 2021, 41(3): 462 − 469. HUANG Z L, ZHANG Z C, CHU S P, et al. Synchronous control of vibrating machinery-material system under excitation of four exciters[J]. Journal of Vibration, Measurement & Diagnosis, 2021, 41(3): 462 − 469.
[23] 陈坚. 交流电机数学模型及调速系统[M]. 北京: 国防工业出版社, 1989. CHEN J. Mathematical model of AC motor and speed control system [M]. Beijing: National Defense Industry Press, 1989.




 下载:
下载:
 下载:
下载:
